Algoritmos Genéticos |
 |
Descargar código |
- Introducción
- Problema OneMax
- Codificación
- Generación de la población incicial
- Evaluación
- Selección
- Explotación Vs. Exploración
- Cruce
- Mutación
- Reemplazo
- Algoritmo genético
- Prueba del Algoritmo Genético
Introducción
El término ''Computación Evolutiva'', ha sido empleado para referirse a la escuela (del pensamiento) que toma la Teoría de la Evolución como inspiración y marco de referencia para diseñar algoritmos heurísticos de búsqueda y optimización. El campo del Cómputo Evolutivo es una aplicación del modelo biológico y la teoría de la evolución de Darwin a la ciencia computacional, y es usada para encontrar soluciones a todo tipo de problemas de búsqueda y optimización.
El aspecto clave que distingue a un algoritmo de búsqueda evolutivo de uno tradicional, es que el algoritmo evolutivo se encuentra basado en poblaciones de posibles soluciones y, a través de la adaptación de sucesivas generaciones, ejecuta una búsqueda dirigida en forma eficiente.
Los Algoritmos Genéticos (AG) son quizá la técnica mas popular en la investigación dentro de la Computación Evolutiva (CE). Los AG, usan una analogía directa con la naturaleza ya que trabajan con una población de individuos, cada uno de los cuales representa una solución factible a un problema dado. A cada individuo se le asigna un valor de fitness ó puntuación el cual está relacionado con la calidad de su solución. En la naturaleza, esto equivaldría al grado de efectividad de un organismo para competir por determinados recursos. Cuanto mayor es el valor de fitness del individuo, mayor es la probabilidad de que este sea seleccionado para reproducirse. La reproducción produce nuevos individuos que comparten algunas de las características de sus padres. Por otro lado, cuanto menor es el valor de fitness, menor es la probabilidad de que dicho individuo sea seleccionado para su reproducción, lo que evitará, que su material genético se propague en sucesivas generaciones. El siguiente pseudocódigo muestra el funcionamiento de un AG canónico.
| |
|
| Pseudocódigo 1: Algoritmo Genético Canonico | |
| |
|
| 1 | GenerarPoblacionInicial(P(0)) |
| 2 | Evaluar(P(0)) |
| 3 | while CriterioParada(P(0)) != falso |
| 4 | P’(t) = Seleccionar(P(t)) |
| 5 | P’’(t) = Cruzar(P’(t)) |
| 6 | P’’’(t) = Mutar(P’’(t)) |
| 7 | Evaluar(P(t)) |
| 8 | P(t+1) = Remplazar(P(t),P’’’(t)) |
| 9 | t = t + 1 |
| 10 | end while |
| |
|
Problema OneMax
Para mostrar el funcionamiento del AG canónico, se resolverá el problema de OneMax que se define como sigue:
Sea la cadena de bits de longitud ‘n’
x =\{x_1,x_2,\cdots,x_n\}
Donde:
x_i \in \{ 0,1 \}
Maximizar la siguiente función:
f(x) = \sum_{i=1}^nx_i
Codificación
En el algoritmo genético clásico (AGC) propuesto por John Henry Holland, cada individuo o posible solución es representado por una cadena de bits de longitud fija. Se asume que cada posición en la cadena representa una característica específica del individuo y el valor almacenado en dicha posición, representa la forma en que se manifiesta dicha característica en la solución.
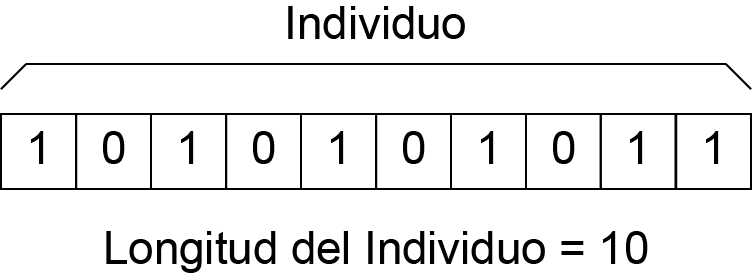
Figura 1: Codificación
Generación de la población incicial
Como ya se menciono anteriormente, un AG está compuesto por una colección de individuos llamada población. El número de individuos que integra dicha población se denomina “tamaño de la población”. El primer paso en el AG canónico, consiste en inicializar dicha población de forma aleatoria con una distribución uniforme.
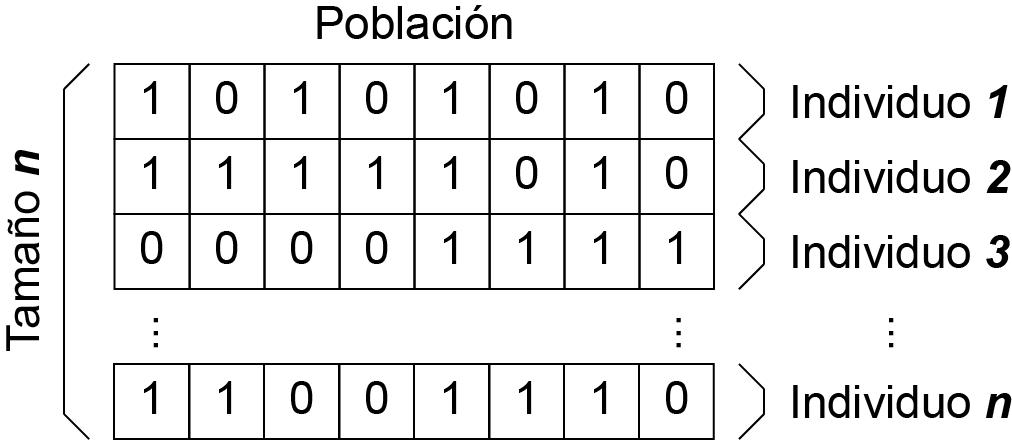
Figura 2: Población
El siguiente código en Matlab, muestra un ejemplo para la implementación de la función “GenerarPoblacionInicial”
function poblacion = GenerarPoblacionInicial(tamano, longitud_individuo) poblacion = randi([0,1],longitud_individuo,tamano); end
Archivo: GenerarPoblacionInicial.m
Para probar el código anterior se puede utilizar la siguiente llamada a la función:
poblacion = GenerarPoblacionInicial(10, 5)
poblacion =
1 1 0 1 1
0 0 0 1 1
0 1 0 1 0
0 1 0 1 1
0 0 1 0 1
1 1 1 1 1
1 0 1 0 0
1 1 1 1 0
1 1 1 0 0
1 0 1 0 1
Evaluación
El AG determina la calidad de un individuo utilizando la “función de fitness” y esta varia dependiendo del problema que se este resolviendo. Para el caso de del problema OneMax la función de fitness calcula la suma total de unos dentro de la cadena de bits.
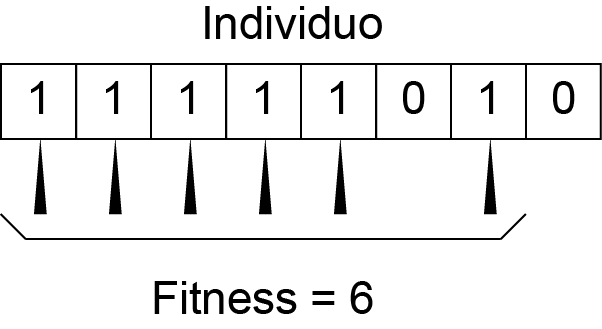
Figura 3: Ejemplo de valor de fitness
El siguiente código en Matlab, muestra un ejemplo para la implementación de la función de fitness para el problema OneMax.
function res = Fitness(individuo)
res = sum(individuo);
end
Archivo: Fitness.m
Para probar el código anterior se puede utilizar la siguiente llamada a la función:
individuo = [1 0 1 1 0]; aptitud = Fitness(individuo) aptitud = 3
Selección
Para poder realizar la operación de cruza, el AG debe seleccionar ciertos individuos de la población. Dichos individuos generalmente son seleccionados con una probabilidad que es proporcional al valor de fitness de los individuos en cuestión, así entonces, los individuos con mejor valor de fitness tienen una mayor probabilidad de ser seleccionados que los de menor valor de fitness, a dicho método se le conoce con el nombre de “método de la ruleta”.
Otro método de selección clásico en los AG es el “torneo binario”. En este, el AG selecciona aleatoriamente y con la misma probabilidad dos individuos de la población, posteriormente se calcula el valor de fitness de cada uno de los individuos seleccionados. El individuo con mejor valor de fitness será el individuo finalmente seleccionado.
| |
|
| Pseudocódigo 2: Torneo binario | |
| |
|
| 1 | I1 = Selección(P(t)) |
| 2 | I2 = Selección(P(t)) |
| 3 | if Fitness(I1) >= Fitness(I2) then |
| 4 | I = I1 |
| 5 | else |
| 6 | I = I2 |
| 7 | end if |
| |
|
El siguiente código en Matlab, muestra un ejemplo para la implementación del método de selección por torneo binario.
function individuo = Seleccionar(poblacion)
i1 = poblacion(randi([1,size(poblacion,1)],1,1),:);
i2 = poblacion(randi([1,size(poblacion,1)],1,1),:);
if Fitness(i1) >= Fitness(i2)
individuo = i1;
else
individuo = i2;
end
end
Archivo: Seleccionar.m
Para probar el código anterior se puede utilizar la siguiente llamada a la función:
individuo = Seleccionar(poblacion)
individuo =
1 0 1 1 0
Explotación Vs Exploración
Como se menciono anteriormente, los AG son algoritmos de búsqueda guiados por probabilidades que permiten obtener buenos resultados en tiempos aceptables, esta es la razón por la que son empleados frecuentemente para resolver problemas de tipo NP y NP completos.
En todo proceso de búsqueda, es importante que se tenga en cuenta dos factores fundamentales: explotación y exploración. El adecuado balance entre estos dos factores permitirá que la búsqueda sea mas o menos eficiente.
Durante el proceso de explotación, el algoritmo realiza (hasta cierto punto) una búsqueda exhaustiva en cierta región del espacio de búsqueda, sin embargo, de vez en cuando es recomendable que el algoritmo busque soluciones en nuevas zonas, lo que permitirá que no se quede atrapado en óptimos locales.
En el caso particular del AG canónico, el proceso de explotación se lleva acabo a través del operador de cruza (con una probabilidad alta, en muchos casos mayor a 0.5) y la exploración se realiza con el método de mutación (con una probabilidad baja la cual generalmente es calculada como 1 entre la longitud del individuo).
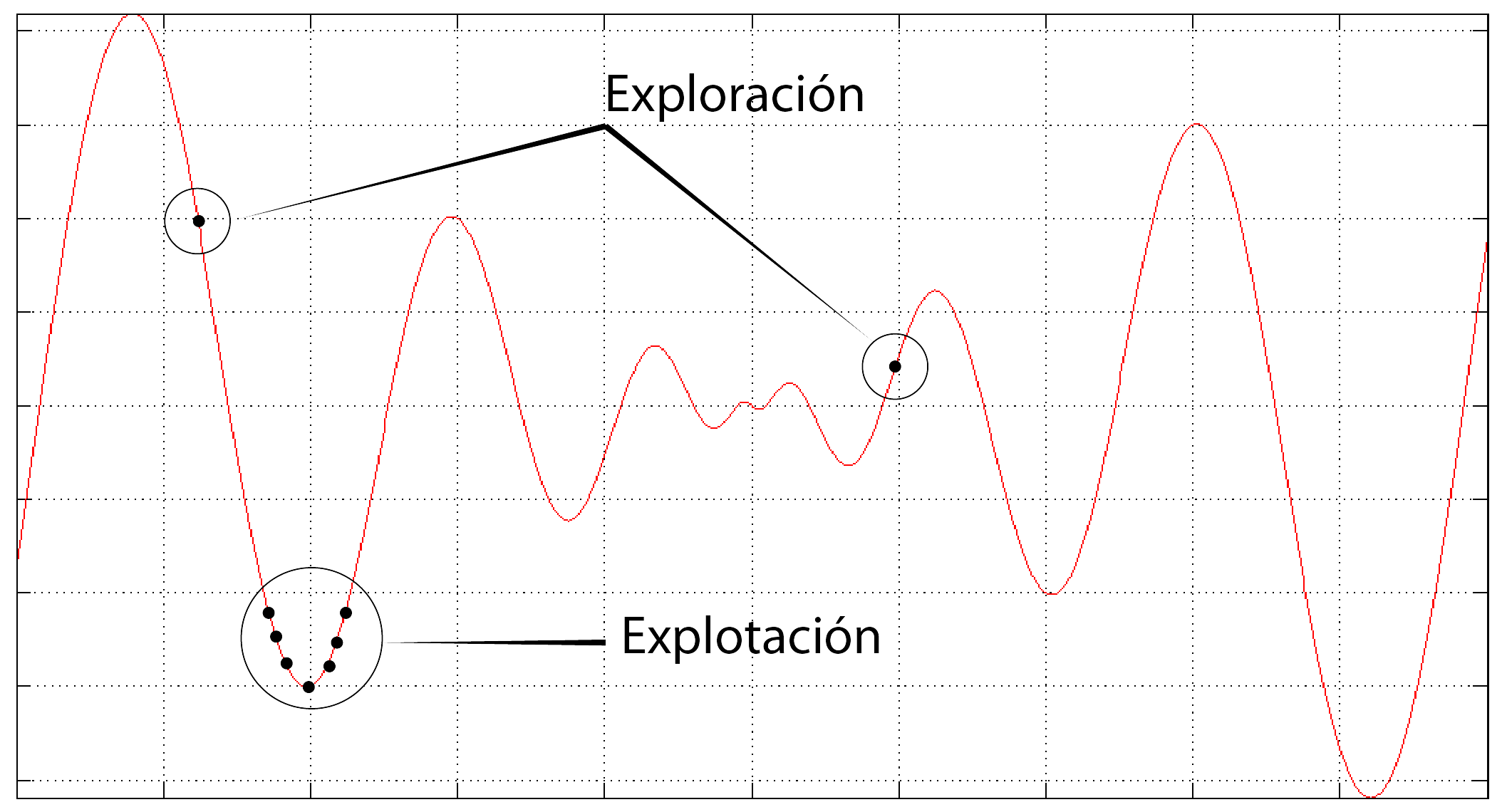
Figura 4: Explotación Vs. Exploración
Cruce
La operación de cruce (también llamada recombinación) tiene como objetivo intercambiar información entre dos padres de tal forma que con el paso del tiempo se vallan heredando las mejores características de cada uno de los padres dando como resultado en muchos de los casos descendientes con mejores valores de fitness que los padres.
Quizá el método de cruza mas utilizado en los AG clásicos sea el denominado “cruza de un punto”. En este, dados dos individuos (padres) seleccionados previamente (por el método de la ruleta, torneo binario, etc) y un punto de cruza generado aleatoriamente, se intercambian las partes de los individuos para generar a los descendientes (Figura 4)

Figura 5: Cruza de un punto
El siguiente código en Matlab, muestra un ejemplo para la implementación del método de cruza de un punto.
function [descendiente1, descendiente2] = Cruzar(padre1, padre2)
punto_cruza = randi([1,length(padre1)]);
descendiente1 = [padre1(1:punto_cruza) padre2(punto_cruza+1:length(padre2))];
descendiente2 = [padre2(1:punto_cruza) padre1(punto_cruza+1:length(padre1))];
end
Archivo: Cruzar.m
Para probar el código anterior se pueden utilizar los siguientes comandos:
padre1 = [1 1 1 1 1 1];
padre2 = [0 0 0 0 0 0];
[individuo1, individuo2] = Cruzar(padre1, padre2)
individuo1 =
1 1 0 0 0 0
individuo2 =
0 0 1 1 1 1
Mutación
La operación de mutación, tiene como objetivo ayudar a que el AG no se quede atrapado en óptimos locales. El método clásico de mutación empleado por los AG, es el denominado “bit flip” que tiene como objeto volver ‘0’ los ‘1’ y viceversa para aquellas posiciones del individuo que hayan sido seleccionadas con base en la probabilidad de mutación.
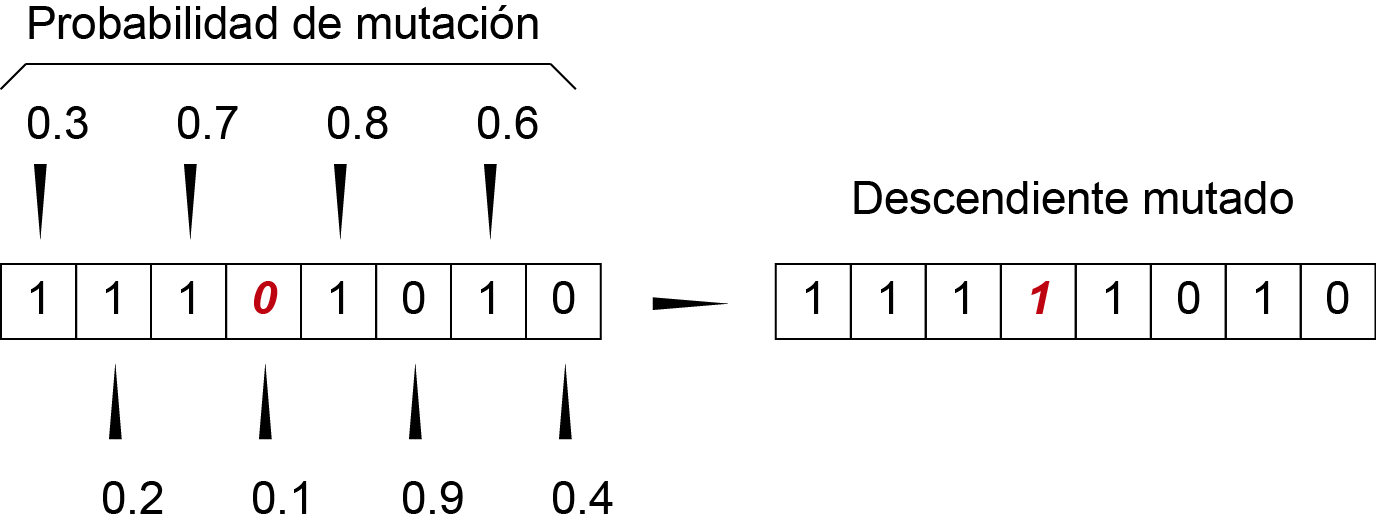
Figura 6: Mutación “bit flip”
function individuoMutado = Mutar(individuo)
pm = 1/length(individuo);
individuoMutado = zeros(1,length(individuo));
for i=1:length(individuo)
if rand() <= pm
individuoMutado(i) = not(individuo(i));
else
individuoMutado(i) = individuo(i);
end
end
end
Archivo: Mutar.m
Para probar el código anterior se pueden utilizar los siguientes comandos:
individuo = randi([0 1], 1,8)
individuo =
0 0 1 1 1 0 1 1
individuoMutado = Mutar(individuo)
individuoMutado =
1 0 1 1 1 0 1 1
Reemplazo
Una vez que los individuos han sido cruzados y mutados, se crea una nueva población que será utilizada durante la siguiente iteración del proceso evolutivo, es decir, se seleccionan aquellos individuos que son mas aptos para seguir adelante y se desechan (mueren) aquellos individuos menos aptos. El siguiente código en Matlab, muestra un ejemplo para la implementación del método de reemplazo muy básico.
function poblacion = Remplazar(poblacion, nueva_poblacion)
for i=1:size(poblacion,1)
if Fitness(nueva_poblacion(i,:)) >= Fitness(poblacion(i,:))
poblacion(i,:) = nueva_poblacion(i,:);
end
end
end
Algoritmo Genético
Una vez que ya se han explicado todos los componentes de un AG canónico, se mostrara el código que implementa el AG para el problema que estamos resolviendo (OneMax).
function poblacion = AG(tamano, longitud_individuo, probabilidad_cruza, iteraciones)
poblacion = GenerarPoblacionInicial(tamano, longitud_individuo);
nueva_poblacion = zeros(tamano, longitud_individuo);
for gen=1:iteraciones
for i=1:2:tamano
individuo1 = Seleccionar(poblacion);
individuo2 = Seleccionar(poblacion);
if rand() >= probabilidad_cruza
[descendiente1, descendiente2] = Cruzar(individuo1, individuo2);
else
descendiente1 = individuo1;
descendiente2 = individuo2;
end
individuoMutado1 = Mutar(descendiente1);
individuoMutado2 = Mutar(descendiente2);
nueva_poblacion(i,:) = individuoMutado1;
nueva_poblacion(i+1,:) = individuoMutado2;
end
poblacion = Remplazar(poblacion, nueva_poblacion);
end
end
Prueba del Algoritmo Genético
Para probar el AG creado anteriormente utilizaremos los siguientes parámetros:
| |
|
| Parámetro | Valor |
| |
|
| Tamaño de la población | 10 |
| Longitud del individuo | 8 |
| Probabilidad de cruza | 0.8 |
| Probabilidad de mutación | 1/8 |
| Criterio de parada | 30 iteraciones |
| |
|
poblacion = AG(10,8,0.8,30)
poblacion =
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
Como se observa en los resultados anteriores, los individuos han evolucionado hasta alcanzar la meta planteada por el problema OneMax que consiste en conseguir el mayor número de unos en cada individuo.
En la siguiente gráfica se muestra el proceso de convergencia del AG cuando se utiliza un individuo de longitud igual a 800 y 10 individuos. Como se puede observar, son necesarias al menos 1400 generaciones para que el algoritmo converja utilizando la siguiente tabla de parámetros:
| |
|
| Parámetro | Valor |
| |
|
| Tamaño de la población | 100 |
| Longitud del individuo | 800 |
| Probabilidad de cruza | 0.8 |
| Probabilidad de mutación | 1/800 |
| Criterio de parada | 200 iteraciones |
| |
|
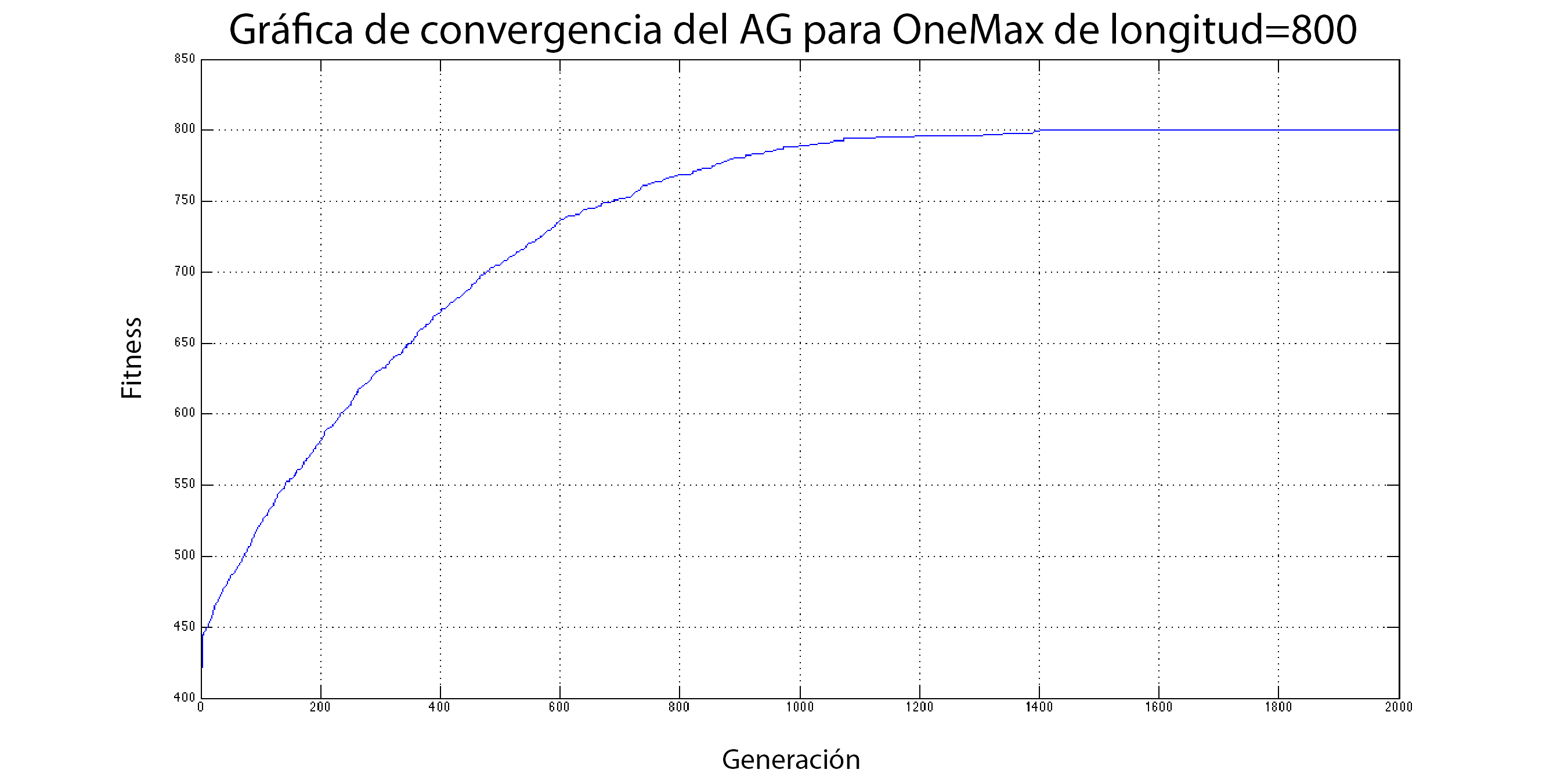
Figura 7: Gráfica de convergencia para una población de 10 individuos
En la siguiente gráfica se muestra el proceso de convergencia del AG cuando se utiliza un individuo de longitud igual a 800 y 100 individuos. Como se puede observar, son necesarias al menos 580 generaciones para que el algoritmo converja utilizando la siguiente tabla de parámetros.
| |
|
| Parámetro | Valor |
| |
|
| Tamaño de la población | 100 |
| Longitud del individuo | 800 |
| Probabilidad de cruza | 0.8 |
| Probabilidad de mutación | 1/800 |
| Criterio de parada | 2000 iteraciones |
| |
|
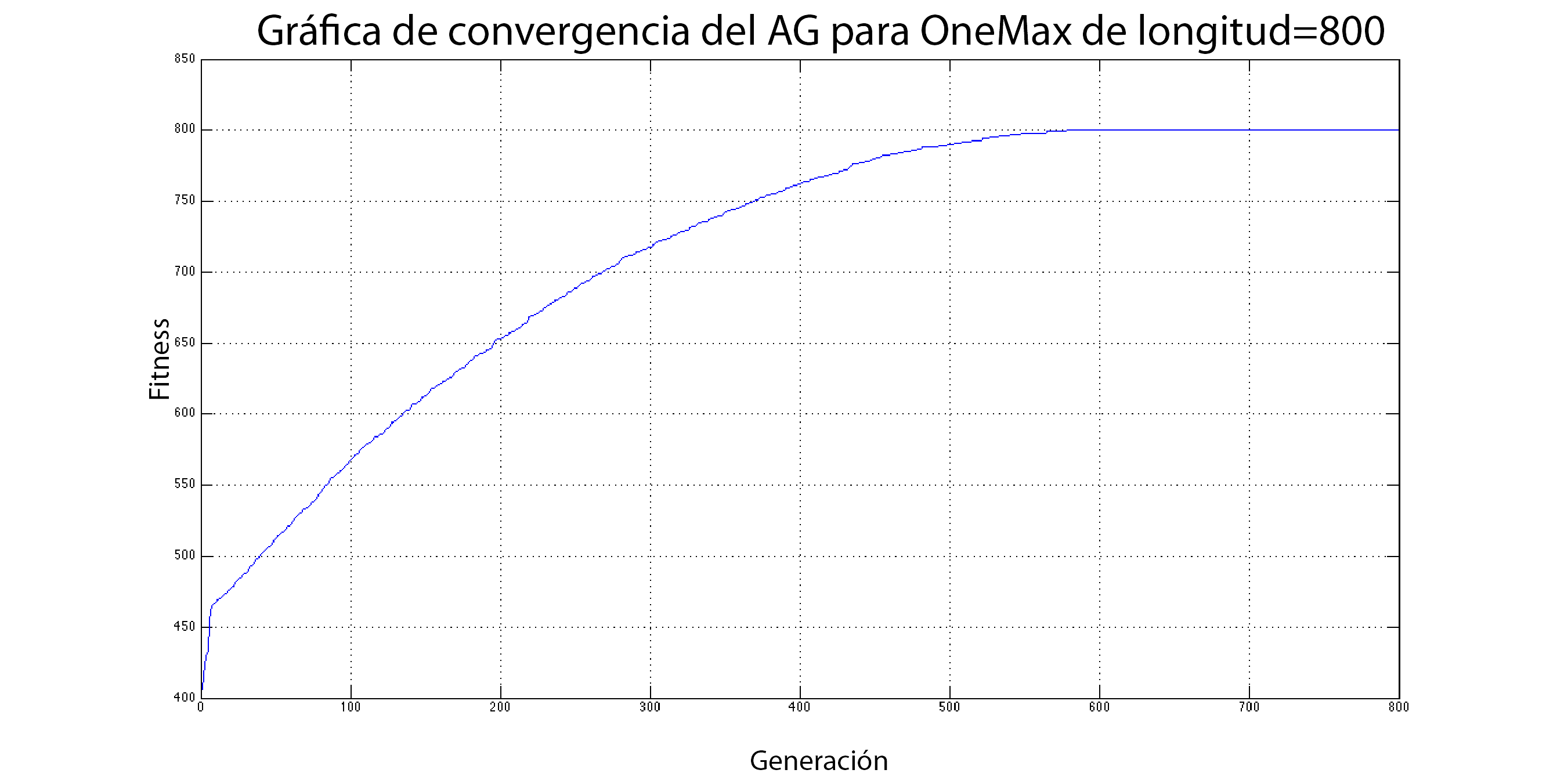
Figura 8: Gráfica de convergencia para una población de 100 individuos
Como se puede observar en las graficas anteriores, la convergencia del algoritmo con 100 individuos es mas rápida que en el caso de cuando se utilizan solo 10 individuos. Lo que se pretende mostrar con esto, es que los valores de los parámetros son fundamentales a la hora de trabajar con los AG.
Se podría pensar que si se aumenta infinitamente el número de individuos de la población, el algoritmo convergiría mas rápido sin embargo esto no es así. También se debería de considerar que pasaría si se utilizaran diferentes probabilidades de cruza y mutación, al respecto, existen numerosas investigaciones y trabajos que intentan responder la pregunta de cuales son los parámetros óptimos o adecuados para los AG sin que se tenga aun una respuesta clara.