III. |
APPLICATIONS OF GENETIC ALGORITHMS |
Contents of this chapter
- III.1 Index of Most Important Applications of the Genetic Algorithms
- III.2 GAs for the Design of Neural Networks
- III.2 GAs in Combinatorial Optimization
III.1 Index of Most Important Applications of the Genetic Algorithms
This section presents a overview of applications of genetic algorithms to real-world problems.
 Genetic Algorithms in Parametric
Design of Aircraft, by Mark F. Bramlette and Eugene E. Bouchard. The authors discuss
optimizing aircraft designs when the task is posed as that of optimizing a list of parameters.
They have approached the problem with a number of optimization algorithms, including a genetic
algorithm using real number representation. They also discuss the performance of each algorithm
and describe some innovative techniques used in their quite successful genetic algorithm,
including the technique of generating a large number of initial population members and then
working only with the best ones.
Genetic Algorithms in Parametric
Design of Aircraft, by Mark F. Bramlette and Eugene E. Bouchard. The authors discuss
optimizing aircraft designs when the task is posed as that of optimizing a list of parameters.
They have approached the problem with a number of optimization algorithms, including a genetic
algorithm using real number representation. They also discuss the performance of each algorithm
and describe some innovative techniques used in their quite successful genetic algorithm,
including the technique of generating a large number of initial population members and then
working only with the best ones.
 Dynamic Anticipatory Routing in
Circuit-Switched Telecommunications Networks, by Louis Anthony Cox, Jr., Lawrence
Davis, and Yuping Qiu. The objective of the study is to optimize the routing of telephone
networks in order to minimize costs to US West. It compares the performance of an order-based
genetic algorithm with several other optimization techniques on this problem. The authors
conclude that the genetic algorithm is a highly successful technique when the problem is
complex, but hybridization of these algoritms can lead to better performance than using any of
them in isolation.
Dynamic Anticipatory Routing in
Circuit-Switched Telecommunications Networks, by Louis Anthony Cox, Jr., Lawrence
Davis, and Yuping Qiu. The objective of the study is to optimize the routing of telephone
networks in order to minimize costs to US West. It compares the performance of an order-based
genetic algorithm with several other optimization techniques on this problem. The authors
conclude that the genetic algorithm is a highly successful technique when the problem is
complex, but hybridization of these algoritms can lead to better performance than using any of
them in isolation.
 A Genetic Algorithm Applied to
Robot Trajectory Generation, by Yuval Davidor. He shows how to apply genetic algorithm
techniques to the task of planning the path which a robot arm is to take in moving from one
point to another. Davidor uses variable-length chromosomes in his solution, and devises some
novel and interesting crossover operators.
A Genetic Algorithm Applied to
Robot Trajectory Generation, by Yuval Davidor. He shows how to apply genetic algorithm
techniques to the task of planning the path which a robot arm is to take in moving from one
point to another. Davidor uses variable-length chromosomes in his solution, and devises some
novel and interesting crossover operators.
 Genetic Algorithms, Nonlinear
Dynamical Systems, and Models of International Security, by Stephanie Forrest and
Gottfried Mayer-Kress, concerns a problem posed by current research in chaotic models of real
processes. Chaotic models of international arms races and economic competition seem to model
some features of the real-world processes better than some other more traditional models have done.
The authors use a genetic algorithm to find good settings of the parameters of
Mayer-Kress's models in order to enhance their performance on the models.
Genetic Algorithms, Nonlinear
Dynamical Systems, and Models of International Security, by Stephanie Forrest and
Gottfried Mayer-Kress, concerns a problem posed by current research in chaotic models of real
processes. Chaotic models of international arms races and economic competition seem to model
some features of the real-world processes better than some other more traditional models have done.
The authors use a genetic algorithm to find good settings of the parameters of
Mayer-Kress's models in order to enhance their performance on the models.
 Strategy Acquisition with Genetic
Algorithms, by John J. Grefenstette. He experiments with SAMUEL, a genetic algorithm
that learns techniques for maneuvering a simulated airplane in order to evade a simulated
missile. The genetic algorithm he describes employs several techniques of interest, including
variable-length chromosomes composed of rules that form a production system. A chromosome is
evaluated by using those rules to maneuver the airplane in simulated interactions between
airplanes and missiles. Grefenstette has built knowledge of the production rule domain into his
operators in clever ways.
Strategy Acquisition with Genetic
Algorithms, by John J. Grefenstette. He experiments with SAMUEL, a genetic algorithm
that learns techniques for maneuvering a simulated airplane in order to evade a simulated
missile. The genetic algorithm he describes employs several techniques of interest, including
variable-length chromosomes composed of rules that form a production system. A chromosome is
evaluated by using those rules to maneuver the airplane in simulated interactions between
airplanes and missiles. Grefenstette has built knowledge of the production rule domain into his
operators in clever ways.
 Genetic Synthesis of Neural Network
Architecture, by Steven A. Harp and Tariq Samad, that describes techniques for encoding
neural network architectures on binary chrmosomes. The authors use variable-length chromosomes
and a variety of other novel techniques. This is a good place to begin in learning how to
combine neural networks and genetic algorithms.
Genetic Synthesis of Neural Network
Architecture, by Steven A. Harp and Tariq Samad, that describes techniques for encoding
neural network architectures on binary chrmosomes. The authors use variable-length chromosomes
and a variety of other novel techniques. This is a good place to begin in learning how to
combine neural networks and genetic algorithms.
 Air-Injected Hydrocyclone
Optimization Via Genetic Algorithm, by Charles L. Karr, that describes the solution of a
design problem by a genetic algorithm using the bit string representation technique. Karr
represents the design of an air-injected hydrocyclone as a list of parameters. An interesting
feature of his approach is the use of a new operator called "simplex reproduction". Karr shows
that a genetic algorithm using this operator is quite effective as a search technique for
finding design parameter combinations.
Air-Injected Hydrocyclone
Optimization Via Genetic Algorithm, by Charles L. Karr, that describes the solution of a
design problem by a genetic algorithm using the bit string representation technique. Karr
represents the design of an air-injected hydrocyclone as a list of parameters. An interesting
feature of his approach is the use of a new operator called "simplex reproduction". Karr shows
that a genetic algorithm using this operator is quite effective as a search technique for
finding design parameter combinations.
 A Genetic Algorithm Approach to
Multiple Fault Diagnosis, by Gunar E. Liepens and W. D. Potter, that discusses the use
of a genetic algorithm for finding the most plausible combination of causes for alarms in a
microwave communication system. The authors use binary chromosomes to represent solutions to a
problem that they show is a type of set covering problem. They show how to incorporate
knowledge about set covering optimization into their genetic algorithm in novel ways, yielding
a high-performance hybrid solution to the problem.
A Genetic Algorithm Approach to
Multiple Fault Diagnosis, by Gunar E. Liepens and W. D. Potter, that discusses the use
of a genetic algorithm for finding the most plausible combination of causes for alarms in a
microwave communication system. The authors use binary chromosomes to represent solutions to a
problem that they show is a type of set covering problem. They show how to incorporate
knowledge about set covering optimization into their genetic algorithm in novel ways, yielding
a high-performance hybrid solution to the problem.
 A Genetic Algorithm for
Conformational Analysis of DNA, by C. B. Lucasius, M. J. J. Blommers, L. M. C. Buydens,
and G. Kateman. It is a development of a genetic algorithm for determining the structure of a
sample of DNA based on spectrometric data about the sample. An interesting "cascaded"
evaluation technique that greatly enhances the efficiency of their evaluation function is used. The
authors use bit strings to encode molecular structures. Their evaluation function measures the
degree to which each decoded structure conforms to the data that have been collected about the
sample. The genetic algorithm evolves a description of molecular structure that is in agreement
with the data collected. The problem of determining biomolecular structure occupies a central
position in the worlds of fundamental and applied chemistry today.
A Genetic Algorithm for
Conformational Analysis of DNA, by C. B. Lucasius, M. J. J. Blommers, L. M. C. Buydens,
and G. Kateman. It is a development of a genetic algorithm for determining the structure of a
sample of DNA based on spectrometric data about the sample. An interesting "cascaded"
evaluation technique that greatly enhances the efficiency of their evaluation function is used. The
authors use bit strings to encode molecular structures. Their evaluation function measures the
degree to which each decoded structure conforms to the data that have been collected about the
sample. The genetic algorithm evolves a description of molecular structure that is in agreement
with the data collected. The problem of determining biomolecular structure occupies a central
position in the worlds of fundamental and applied chemistry today.
 Automated Parameter Tuning for
Sonar Information Processing, by David J. Montana. An application of genetic algorithms
to two problems associated with interpreting passive sonar data. The first is a parameterization
problem. To solve it, Montana uses a floating-point version of OOGA to find good parameter settings
for the algorithms employed in the process of interpreting sonar data. The second problem
is a classification problem. For this problem, a genetic algorithm is used to train neural
networks classifying sonar signals in various ways. In this second system, Montana and
Davis experiment with a number of domain-based operators, including the use of
backpropagation -a neural network technique- as a genetic algorithm operator. This appliction
is useful if you are interested in hybrid genetic algorithms, real number representations for
parameterization, or neural networks.
Automated Parameter Tuning for
Sonar Information Processing, by David J. Montana. An application of genetic algorithms
to two problems associated with interpreting passive sonar data. The first is a parameterization
problem. To solve it, Montana uses a floating-point version of OOGA to find good parameter settings
for the algorithms employed in the process of interpreting sonar data. The second problem
is a classification problem. For this problem, a genetic algorithm is used to train neural
networks classifying sonar signals in various ways. In this second system, Montana and
Davis experiment with a number of domain-based operators, including the use of
backpropagation -a neural network technique- as a genetic algorithm operator. This appliction
is useful if you are interested in hybrid genetic algorithms, real number representations for
parameterization, or neural networks.
 Interdigitation: A Hybrid
Technique for Engineering Design Optimization, by Gilbert Syswerda. An application of
a genetic algorithm to the problem of scheduling activities in a laboratory in which each
activity may affect the others in a variety of ways. Syswerda has been implementing this
system under contract to the U. S. Navy. The genetic algorithm uses an order-based chromosome
to represent its schedule. The chromosome is decoded with a decoder that incorporates a good
deal of knowledge about the scheduling domain.
Interdigitation: A Hybrid
Technique for Engineering Design Optimization, by Gilbert Syswerda. An application of
a genetic algorithm to the problem of scheduling activities in a laboratory in which each
activity may affect the others in a variety of ways. Syswerda has been implementing this
system under contract to the U. S. Navy. The genetic algorithm uses an order-based chromosome
to represent its schedule. The chromosome is decoded with a decoder that incorporates a good
deal of knowledge about the scheduling domain.
 The Traveling Salesman and
Sequence Scheduling: Quality Solutions Using Genetic Edge Recombination, by Darrell
Whitley, Timothy Starkweather, and Daniel Shaner. The authors describe a technique for solving
the traveling salesman problem, a well-known combinatorial optimization problem. Their solution
includes novel and ingenious representation, crossover, and repair mechanisms. They also show how
similar techniques can be applied to the problem of scheduling a Hewlett-Packard production
line.
The Traveling Salesman and
Sequence Scheduling: Quality Solutions Using Genetic Edge Recombination, by Darrell
Whitley, Timothy Starkweather, and Daniel Shaner. The authors describe a technique for solving
the traveling salesman problem, a well-known combinatorial optimization problem. Their solution
includes novel and ingenious representation, crossover, and repair mechanisms. They also show how
similar techniques can be applied to the problem of scheduling a Hewlett-Packard production
line.
III.2 GAs for the Design of Neural Networks
(Alba, Aldana, Troya, 1993)
III.2.1 Introduction
Artificial Neural Networks (ANNs) represent an important
paradigm in AI dealing with massively parallel information processing proposed
as biological models for the human brain. ANNs are widely used to offer
human-like skills where they are needed, so we can find them in pattern
recognition, signal processing, intelligent control and many other applications
that can be faced by introducing a network as the heart of the solution
system (see (Kim, Lee, Kim, Hwang, 1991)).
Wherever an ANN is to be used it must first be designed.
At present, any ANN design drags along an unstructured, heuristic and arbitrary
path in order to reach "the better" structure and connectivity
to be trained. Only the training methods are truly applied, but every ANN
type seems to need a different own training mechanism. Usually the training
mechanism is some kind of hillclimbing prosecution, that is very closely
related to (and so, dependent on) the problem being solved, the ANN type
and/or the pattern set for it. The final result is a vast landscape of
different multiparameter tuning procedures to be carried out for any individual
problem and with no warranties for optimum results.
This lack of methodology and the hope of a general multifaced
quasioptimum training made Genetic Algorithms (GAs) suitable for our purposes.
Defined by J. Holland in 1975 GAs simulate natural evolution. In (Goldberg, 1989),
(Whitley, 1989) and (Whitley, Starkweather, Bogart, 1990) can be found the
basis of our GA and ANN approaches. For our purposes chromosomes will encode
ANNs, genes will encode the items being optimized (weights, links or hidden
layers) and alleles will be gene components (regarding upon the used coding
one or more alleles are included to compose a single gene value). Initial
strings will be genetically evolved over generations of newly created offsprings
searching for an optimum.
Because any ANN must be coded as a chromosome string ANN
independence is achieved, just some evaluation procedure must be
defined to recognize relative fitness of individuals to the problem. GA
techniques have a stochastic behaviour and so we only can expect quasioptimum
(very frequent good or optimum) trainings. Besides local minima avoiding,
generality, multiple points parallel search and robutness we can get further
in using GAs to complete ANN design. Since GAs work on some coding of the
solution and not on the solution itself, we can code "any" problem
as a string of parameters and submit it to genetic optimization. Thus,
it is only necessary to properly code ANN connectivity and structure
as strings and define an evaluation procedure to get two new levels of
ANN design. This way we can bring optimization methodology to these two
design stages. This full three level design is thought to help designer's
work from the problem specification (patterns) up to a quasioptimum ANN
to solve it (that is called a Genetic ANN). These three levels of
design will be fully accomplished by using Genetic Algorithms. An introduction
to genetic ANNs can be found in (Mühlenbein 1989) and in
(Mühlenbein 1990).
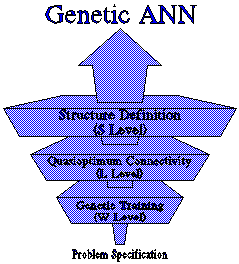
Figure 1. Three Level GANN Design.
We have designed and built up a genetic tool called G.R.I.A.L.
(Genetic Research In Artificial Learning)
(Alba, Aldana, Troya, 1992) to implement several known and new GA techniques
and the three level genetic ANN design in order to test their efficacy
and properties. We are furthermore concerned with scalability and computational
efficiency, thus we have used a Concurrent Logic Language called PARLOG
to implement GA and ANN behaviour in GRIAL as a new kind of computational
approach in the aim of profiting from the outcoming parallelism advantages.
The used test suite is made up of four problems. The XOR
and the Two-bits Binary Adder (TBA) problem (but with 4 patterns) as presented
in (Whitley, Starkweather, Bogart, 1990). A feedforward network to make Spanish Plurals (three
classes classification) and a Hopfield network to behave as a 9-characters
recognitor. The XOR and TBA problems are fully tested (training, connectivity
and layered structure, either separately and together). The Spanish Plurals
ANN has been trained and structure-optimized and the Hopfield network has
been trained. While trying to get the optimum ANN for every problem we
have tested the relative influence of the multiple GRIAL techniques.
In this work we have tested in GRIAL the effects of the
traditional selection procedure versus a one-at-a-time selection
procedure. We explore the influence of coding on ANN design by using binary,
real and a diploid genotypes (this last never tested before for ANN
design). A migration scheme and an adaptive mutation similar
to those used in (Whitley, Starkweather, Bogart, 1990) are tested against sequential single
GAs and constant mutation. A smooth bit climber-like operator (Davis, 1991)
called GBit is tried and a Mating Restriction similar to
(Deb, Goldberg, 1989) is implemented. Dislike partial genetically defined
ANNs (as (Whitley, Starkweather, Bogart, 1990) where genetic training and connectivity are
addressed as separate works and (Harp, Samad, Guha, 1989) where structure
is genetically defined but backpropagation is used for training) we have
designed a full genetic and automatic ANN designer in order to optimize
any ANN component.
III.2.2 PARLOG
PARLOG (Clark, Gregory, 1986) is a Concurrent Logic
Language which has been developed at the Imperial College. Operationally
the computational model of this kind of language consists in a concurrent
processes set which communicates by means of binding logic variables and
which synchronizes by waiting for unbounded logic variables. The possible
behaviors of a process are defined by means of guarded horn clauses: Head
<- Guard : Body. Head and Guard defines the conditions under which
a reduction can be made. Body specifies the resulting state of the processes
after the reduction.
Parlog is one of these languages which exploit two kinds
of parallelism: stream and-parallelism and or-parallelism. The first type
of parallelism occurs when a goal is reduced to a conjuction of subgoals
and they are all tested in parallel. The second type of parallelism appears
when a predicate can be solved by more than one clause. In this case, all
of them are tested at the same time and, if more than one fulfils its guard,
one of them will be selected in an indeterministic way. Parlog also has
some primitives which can be used to avoid both types of parallelism (see
(Crammond, Davison, Burt, Huntbach, Lam, 1989)).
This kind of language fits very well in the parallel programming
paradigm. In opposition to sequential logic languages which present a transformational
behaviour, concurrent logic languages are well fitted to the specification
of reactive system, that is, of open systems which have a high level of
interaction with their environment. And, as stated in (Troya, Aldana, 1991)
, this is what a neural network does: it tries to reach a statistical
minimum that is environment- dependent.
GRIAL is oriented to provide an easy changing of the GA
strategies used to solve a given problem. Unix parallelism is achieved
at interlevel communications while Parlog parallelism appears
at intralevel searchs. Real LAN distribution of intralevel Parlog
parallelism can be faced by using Parlog mail-boxes. Parlog allows entering
parallelism from string managing genetic operations till ANN neurons activations.
Fine and coarse grained approaches are of a straightforward implementation
with Parlog. These advantages along with its lists and symbols processing
make Parlog a better language than imperative ones to get good and reliable
implementations.
III.2.3 Full Genetic ANN Design
In this section a three level and full genetic ANN design
is presented and analyzed by means of GRIAL. New and existing GA techniques
have been tested to get a qualitative understanding of the properties of
this kind of design. We envisage the following exposition from bottom (genetic
training) to up (genetic structure definition) passing through an intermediate
genetic connectivity definition level.
III.2.3.1 Genetic Training
To submit any ANN type to genetic training we must define some proper coding for weights to
appear as strings. GA's work needs some local logic meaning to be present in strings, i.e. a
chromosome must be coded to include logic building blocks with some meaning for the
underlying problem (Goldberg, 1989).
Then we code any ANN string as being a sequence of its input link weights to every neuron in the
ANN, from the input layer to the output layer. The genetic crossover of two different strings
(coded ANNs) profits from their best slices to create better trained offsprings. Through natural
selection bad schemata (bad structures of the solution) are exponentially discarded and
good schemata are exponentially reproduced as evolution occurs. To evaluate the fitness of a
string to the environment (problem) strings are expressed (decoded) as ANNs. We
use SQE (squared error between desired and obtained outputs extended to any output
neuron and any pattern in the pattern set) as the fitness measurement to help natural
selection's work: stochastic selection picks up the best strings to be crossed (reproduced) to
yield offsprings in next generation.
Weights can be coded in strings attending to several codes.
Binary code (signed magnitude) is very extended in genetics. Real,
Reordering and Diploid (Goldberg, 1989) codings are another
known ones we have tried for ANN training. Binary code is very good for
GA job but for ANN training it needs too large populations and evolutions
even for very small problems (we want to keep population size on hundreds
of individuals). Reordering schemes (genes, PMX and/or Inversion) do not
seem to improve binary results, and we think this is because we are using
a correct genotype representation of the problem that does not need additional
genetic help. Real codings (one-weight/one-real-gene) seems to be the true
useful genotype because they allow small and quick GAs to solve adequately
the trainings, despite they present an undesired low diversity maintenance
during evolution that provoques local minima appearences. All these codings
are Haploid codings (one string encodes one ANN), but Diploid
chromosomes with triallelic values (Goldberg, 1989) (and maybe with real values...)
have much to say in allowing sophisticated behaviour by helping diversity
and natural adaptation to traumatic changes in the environmental conditions
(they outperform the other codings using half the number of strings).
Any feedforward, recurrent, dynamic, static or any other
ANN type can be trained by GA means. We have tried constant and
adaptive mutation operators (this last based on Hamming Distance
-hd-) to maintain diversity in population. We think that mutation is not
a secondary operator but an essential technique, very useful in keeping
population size at a relatively low value. Probability for adaptive mutation
is computed as 1/hd (linear) and we have detected this as a somewhat high
value (high mutation has allowed good searches with our one-at-a-time selection),
but in GRIAL, a control technique called begin-end-frequency allows
a better pursuit of GA strategies' effects by specifying how and when to
apply them. In order to speed up the search of a quasioptimum weights set
we have designed the GBit operator, a hybrid genetic-hillclimbing
procedure that makes smooth changes in the best-to-now solution string
to explore its neighborhood. Crossing two strings is not a trivial operation
because these two strings may represent different functionality-neurons
distributions for the problem solution and crossover will often yield two
new strings (ANNs) that behave much worst than their parents and that are
unable of future improvement (called Lethal strings). To solve this
problem we have designed a Restrictive Mating operator based on
hamming distance (similar to the Genotypic Mating Restriction described
in (Deb, Goldberg, 1989) to impose a minimum likeness between mates to
be sure that interspecies (very different couples) crossovers do not take
place. This problem is very frequent in big populations where many good
but different partial solutions often appear. GBit and RMating have shown
to turn GAs quick tools of high efficacy. Since ANN coding/decoding and
evaluation operations are very complex and expensive we look for improved
selection mechanisms that minimize wanderings along the search space while
maintaining GA properties. The Generations Evolutive Scheme (a full
new generation replaces the old one) using the Stochastic Remainder
Without Replacement seems to be very expensive in our tests despite
its advantages in preserving diversity and genotype exploration. That's
why we have designed the Immediate Effects Evolutive Scheme to keep
strings ranked (from best to worst) and using the Roulette Wheel
selection to pick up two individuals to be genetically processed and produce
offsprings to be inserted in the ranking. This later selection operator
is the best choice for ANN design, but population size must be kept large
enough to avoid premature convergence due to its more minimum-directed
search. A complete-ranked selection as that in (Whitley, 1989) could lessen
genetic drift because in GRIAL we allow duplicates in the population and
the IEES produces a high selection pressure.
We have finally tested and stated the superiority of any
Distributed search using N GAs over any equivalent single GA search
for the whole test suite. We have used a Migration scheme similar
to (Whitley, Starkweather, Bogart, 1990) to define N GAs in parallel evolution with occasional
exchanges of their respective best strings through Parlog streams. This
parallelism improves time, accuracy, diversity, lethals avoiding and is
more likely to yield a quasioptimum result. Real speed-up for quick GA
evolutions can be brought from real machine distribution of the N GAs in
a LAN or multiprocessor computer.
III.2.3.2 Connectivity Optimization
In traditional ANN design connectivity is determined by
the ANN type to be used or by experience. We want to make a genetic
connectivity definition to accomplish three goals: (a) GAs are
used to define connectivity and weights (training), (b) we want
our method to be scalable with problem size and (c) the predefined
structure to be connected must be full used, because we expect this structure
to have been selected as quasioptimum by any means.
By coding links in strings we want to obtain the GAs advantages
not only in that links pruning is tried but links appear and disappear
in parallel in strings as evolution occurs. Binary codings as the used
in (Whitley, Starkweather, Bogart, 1990) fill every string position to encode presence (1)
or absence (0) of a link, but this coding yields excessively long chromosomes
that do not scale as the problem grows because, even if the GA discovers
the useless links, the strings must hold room enough to contain
the full link space. To allow designer deciding the magnitude of the search
to be carried out we only impose a low and high limit to GA strings length
to encode links (regarding the ANN structure).
We have designed a General Artificial Neuralnetwork
sheet (GAN) as an implicit link space for feedforward and/or recurrent
ANNs. For a given ANN structure three GAN input link spaces are defined:
FF (feedforward), FK (feedback) and DIO (direct-io)
input link spaces. We associate every link with its weight value through
the use of symbolic genes we call wlink genes to allow independent
existence of any link in the ANN. Every string of wlink genes in the
GA population encodes a subset of the full link space being optimized.
The user of GRIAL can specify the way and strings length
in which link subsets are encoded. Thus, designer can specify the length
of strings in the population, then pruning as desired the full link
space. Excessive initial pruning has shown to be undesirable because networks
are unable to learn the full pattern set. The rational use of the ANN structure
brings from the results one can get by pruning links beyond a low limit:
many neurons can be present in the final ANN whose input and/or outputs
are not being considered when the ANN works. So we have defined Archetypes
as distinguished string positions respected by the crossover during evolution.
Archetypes assure that the ANN structure is being profited by
This linking (L) level uses the training (W) level to
determine weights and fitness for its initial population and evolution
is responsible for crossing the subsets of links (strings) looking for
a quasioptimum solution. Link pruning and adding are achieved by a link
duplication effect. We have tried penalty schemes attending to links
number in order to modify the fitness values, but results indicate that
any other penalty schemes (as giving more -W- learning facilities to strings)
should be of greater success. But the real power of this technique becomes
from the initial designer-drived pruning and the subsequent GA optimization.
Again the best results are these obtained with N distributed GAs working
in parallel. At L level we pretend to make a more natural ANN design by
interacting with the training lower level and then making it easy as well
as more accurate and cheaper to implement (as software or hardware ANNs).
III.2.3.3 Structure Definition
Defining the best ANN structure for a given problem is
not a deterministic nor even a well known process due to the complexity
of recognizing every neuron job in the whole ANN and the relationships
among neurons. There exist many rules based on experience about the number
and disposition of neurons, but, as for connectivity definition, designers
have not a methodology out of the proof-and-error mechanics.
The real problem for a genetic structure definition is
to select a good coding to contain structure information, general
enough to be combined by crossover and specific enough to determine one
unique ANN structure when decoded (expressed). We have designed a pure
binary genotype to do this job (a strong coding of the structure).
We want to optimize the number of hidden layers and neurons per hidden
layer. GRIAL puts in a chromosome one gene for every one of the GN
potentially existing hidden layers, and the genes length (GL) determines
the maximum number of neurons per hidden layer. Then if we want between
0 and GN hidden layers and between 0 and 2GL-1
neurons per hidden layer we should use binary chromosomes of GN*GL length
in the Structuring (S) level.
We have got very good results for feedforward and GAN
networks regarding useless hidden neurons pruning (in order to reduce the
cost per ANN) and quasioptimum structures generation (e.g. we have genetically
duplicated the human proposed structure for the XOR problem). Furthermore
a penalty scheme based on changes in the fitness values according
to the neurons number of the network has been successfully tried with some
interesting side effects in helping natural selection decisions while searching
for smaller and cheaper ANN structures.
Usually the kind of desired structure is best known by
the designer than the best connectivity pattern or even the weights set
to be used, and that's why S level search is accomplished by smaller GAs
than those GAs needed at L or W levels. On the other hand S strings are
very complex and expensive to evaluate for fitness because they require
multiple L and/or W GAs executions. Genetic operators have been extended
to this level (e.g. GBit or mutation) but the simple traditional GA has
shown to be a good procedure for S level. We encourage the use of the Immediate
Effects Evolutive Scheme in order to prevent useless wanderings even
when we risk to obtain only good structures and not the best ones. For
structure definition, hillclimbing-like methods may reduce the overall
cost.
The final best ANN will have been designed taking account
for many aspects to yield a full suited ANN to the proposed environment
(the problem). Individual GAs will gain by being allowed to present a higher
rate of error due to the multiple level relationships (GA parameters tuning
does not need to be of high accuracy to work well). As we can see the parallelism
at many computational levels is the best way to bring efficiency and efficacy
to this complex Genetic ANN design: three levels run in parallel, several
GAs can work in parallel at any level and every genetic operation can be
parallelized due to PARLOG software enhancement. PARLOG can be used to
define an Object Oriented library of ANN simulators (Troya, Aldana, 1991)
and to implement any kind of GA parallelism as those mechanisms outlined
in (Macfarlane, East). GRIAL includes some of these propositions.
III.2.4 Conclusions
There exist many different non GA ways to define the target
ANN to solve a problem and many other Evolutive mechanisms but the Full
Three Levels ANN Design is thought to be the best and more natural
way to take designer to quasioptimum ANNs by controlling only some GA strategies.
GAs provide the better set of tools to do this work. Resulting ANNs can
be later refined by any of the appliable existing mechanisms.
We think that a smart connectivity for initial pruning
to be used at L strings (initial link strings composition) can improve
the connectivity definition, because, when full automatic design is being
performed, S level randomly generates this pruning and only a high number
of strings at S level can overcome excessive initial pruning (because numerous
initial prunings are to be tested).
The "best" GA to ANN design is a distributed
search with IEES or a similar ranked selection, using a somewhat high mutation
rate, two point crossover and some help to avoid lethals and to speed up
search (GBit or another bit climber and some niche & species formation
technique like RMating if no migration is to be used).
ANNs and GAs are thought to be open and reactive systems
which fit very well whithin the logic and the concurrent programming paradigms.
Thus, many advantages regarding parallel implementations and software improvements
can be brought from the use of Parlog as the base language.
With the correct combination of our GA techniques or some
extensions of them we can define a general methodology to enter automatic
ANN design in a unified fashion while still maintaining diversity of approaches
to solve a problem. Computational requirements of this kind of design (through
genetics) are to be enhanced by parallelism in order to reduce the time
and memory consuming GAs that we are still forced to use in solving large
problems.
III.3 GAs in Combinatorial Optimization
There exists an extensive range of problems which can be formulated as obtaining the values
for a vector of variables subject to some restrictions. The elements of this vector are
denominated decision-variables, and their nature determines a classification of this kind of
problems. Specifically, if decision-variables are required to be discrete (i.e. the solution
is a set or sequence of integer numbers or any other discrete type), the problem is said to
be combinatorial. The process of finding optimal solutions (maximizing or minimizing an
objective function) for such a problem is called combinatorial optimization.
Combinatorial optimization problems have been traditionally approached using exact techniques
such as Branch and Bound (Lawler and Wood, 1966). Finding the
optimal solution is ensured with these techniques but, unfortunately, they are seriously limited
in their application due to the so-called combinatorial explosion. As an example,
consider the Travelling Salesman Problem (TSP). This problem (obtaining a minimal
Hamiltonian tour through a complete graph of n nodes) is a classical example of NP-complexity:
the work-area to be explored grows exponentially according with the number of nodes in the graph,
and so does the complexity of every know algorithm to solve this problem. It is not only a good example
of a combinatorial optimization problem, but also an approach to real problems like
VLSI-design or X-ray crystallography (Reinelt, 1994).
III.3.1 Genetic Algorithms to solve the TSP
Building a genetic algorithm to solve the TSP requires specifying those elements described
in the GA definition. However, here only the really TSP-specific elements will be described since
others (such as selection and replacement functions) are normally problem-independent.
III.3.1.1 Fitness function
This element is here very simple. In fact, it suffices to assign each string a fitness value
equal to the cost of the whole tour. As this function is to be minimized, that value must be
inverted or, ever better, be subtracted from the fitness value of the worst individual in the
population (whose new fitness will consequently be 0). An aspect to take in account is the
apparition of scaling problems since, as the population evolves, differences between solutions
tend to be smaller and even negligible in relation with the absolute values of them. So it is
necessary to realize some kind of a normalization process in order to amplify that difference
and guide more efficiently selective pressure.
III.3.1.2 Representation function
A first classification of the representation functions existing for the TSP partitions them
into binary and non-binary functions.
Binary encoding fits to the most classical GA model. In this one, each node is represented
by a segment of n bits (n is a natural number obtained from rounding up by excess
log m, where m is the number of nodes), and a solution by an ordered sequence of
such segments. This encoding has many problems.
m, where m is the number of nodes), and a solution by an ordered sequence of
such segments. This encoding has many problems.
First, if the number of nodes is not a power of 2, there exists segments without a
corresponding node and, as a result, non-valid binary strings. Second, any operator working on
this encoding should consider the segments corresponding to each node as atomic units;
in any other case many non-valid strings would been generated. Although some positive results
have been reported using this representation
(Michalewicz, 1992), it is usually less efficient and
performs worse than other encoding functions.
Non-binary encodings use an alphabet with n symbols (n is the problem size) to
represent solutions for the problem. There exist some options to encode: path, adjacency and ordinal.
 Path encoding is the most intuitive one:
every node is assigned a number (e.g. from 0 up to n-1) and solutions are represented
by the ordered sequence of visited nodes.
Path encoding is the most intuitive one:
every node is assigned a number (e.g. from 0 up to n-1) and solutions are represented
by the ordered sequence of visited nodes. Adjacency encoding uses each position in the
string to represent an edge of the tour. So, if jth position of the chromosome contains
the value k, the edge (j,k) belongs to the tour.
Adjacency encoding uses each position in the
string to represent an edge of the tour. So, if jth position of the chromosome contains
the value k, the edge (j,k) belongs to the tour. Ordinal encoding is the third option. Using
it, each solution is represented by a list of n values, such that the ith
position of it cannot contain a higher value than n-i, due to the fact that every gen
points to a position within a stack from where visited nodes are progressively extracted.
Initially, the stack contains all nodes in a fixed, predetermined, arbitrary order.
Ordinal encoding is the third option. Using
it, each solution is represented by a list of n values, such that the ith
position of it cannot contain a higher value than n-i, due to the fact that every gen
points to a position within a stack from where visited nodes are progressively extracted.
Initially, the stack contains all nodes in a fixed, predetermined, arbitrary order.
Basic features of the encodings above are detailed in
(Michalewicz, 1992) and
(Suárez, 1994). There is a third way to
encode tours, matrix encoding, which has some varieties too. Since the size of matrixes
grows according to the square of the problem size, they require a large amount of space. A
description of these representations and their associated operators can be found in
(Michalewicz, 1992).
III.3.1.3 Operators
The next point to specify is the available operator set. It is very dependent of the
encoding function used since some operators are more appropriate for a determined
representation and others are not applicable to it at all. In order not to make this section
too extensive, only operators for path and adjacency encodings are described. Operators for
ordinal and binary representations can be found in
(Suárez, 1994).
First, crossover operators for adjacency encoding are described. As mentioned, a crossover
operator must produce one or more offsprings combining information of, usually, two ancestors.
A synergyc recombination of this information is the way to achieve improvements in the
solutions provided by the algorithm. The most classical operators working on this
representation are:
- Alternating-Edges Crossover
- Subtour-Chunks Crossover
- Heuristic Crossover
For path encoding, the most notable operators are:
 Partially-Mapped Crossover or PMX
Partially-Mapped Crossover or PMX- PMX is an operator proposed by Goldberg and Lingle
(1985). It is designed to preserve many absolute positions from both parents. It works selecting two cutpoints in the first parent
and copying the elements between them. This transfer also defines a set of mappings between the elements that have been
copied and the elements in the corresponding positions in the second parent. Then, the rest of elements are copied in the
positions they occur in the second parent. If one position is occupied by an element already copied from the first parent, the
element provided by the mappings is considered. This process is repeated until the conflict is solved.
 Cycle Crossover or CX
Cycle Crossover or CX- CX is an operator that was proposed by Oliver et al. (1987). It generates offspring in which every position
come from one of the parents. Its functioning is based in the concept of cycle. A cycle is a minimal subset of elements
such that the set of positions in which they appear is the same in both parents. This implies that it is possible to switch that
subset from one parent to the other one while keeping a valid permutation. This operator copies the cycle that contains the first
element of the first parent in the positions in which they occur in it, taking the rest of positions from the second parent.
 Order Crossover or OX
Order Crossover or OX- There exist three different variants of OX.
The first variant of order crossover operator (OX#1) was first proposed by
Davis (1985). It works selecting two cutpoints into the sequence, copying the elements between these points from one parent and
preserving the relative ordering of the rest of elements in the second parent, starting after the second cutpoint and considering the
sequence as a ring.
The second variant (OX#2) was proposed by Syswerda (1991). This operator selects some positions at random
in the first parent and copies them into the offspring. The remaining positions are taken from the second parent, starting from the
beginning and respecting their relative ordering.
Finally, the third variant (OX#3) was also proposed by Davis (1991b)
and combines the features of the two operators above. As the first operator, two cutpoints are selected and the elements between them
are copied. As the second operator, the rest of elements are copied from the beginning of the second parent respecting their
relative ordering
The main problem of the operators above is the low percentage of ancestor's edges appearing
in the offsprings, as they usually work with absolute positions of nodes instead of focusing on
edges between them. This causes that an operator to build an offspring just with edges from the
ancestors be defined (Edge-Recombination Crossover). However, path encoding is too poor
for it, so it is completed with an auxiliary structure called edge-map. Detailed descriptions
of this and all operators above can be found in
(Davis, 1991b),
(Michalewicz, 1992) and
(Suárez, 1994).
On the other hand, there are mutation operators. They perform a secondary but decisive role
in the global functioning of the algorithm. Without the renovation of the genetic stuff they
inject into the population, selective pressure would guide crossover operator to produce a
degenerate population. The most significant mutation operators for the path encoding are:
 Inversion: two random points within the
string are selected and the segment between them is inverted. This operator put in two new
edges in the tour.
Inversion: two random points within the
string are selected and the segment between them is inverted. This operator put in two new
edges in the tour. Insertion: a node is extracted from the tour
and inserted in a random position of the string. This operator introduces three new edges in
the offspring.
Insertion: a node is extracted from the tour
and inserted in a random position of the string. This operator introduces three new edges in
the offspring. Shift: it is an extension of the later in
which a segment is extracted. Three new edges are inserted in the tour.
Shift: it is an extension of the later in
which a segment is extracted. Three new edges are inserted in the tour. Reciprocal exchange: the values contained in
two random positions are exchanged, thus introducing four new edges in the string (or two if
the positions to exchange are consecutive).
Reciprocal exchange: the values contained in
two random positions are exchanged, thus introducing four new edges in the string (or two if
the positions to exchange are consecutive). Neighbour exchange: it exchanges the
contents of two consecutive positions within the string, so it may be considered as a
restricted version of the reciprocal exchange or the inversion operator, in that cut or
exchange positions are always consecutive.
Neighbour exchange: it exchanges the
contents of two consecutive positions within the string, so it may be considered as a
restricted version of the reciprocal exchange or the inversion operator, in that cut or
exchange positions are always consecutive.
There are not many references to mutation operators for adjacency encoding, so a path
operator is frequently adapted. Descriptions of such adapted operators can be found in
(Suárez, 1994).
This page was last updated on 21-Nov-97
 Genetic Algorithms in Parametric
Design of Aircraft, by Mark F. Bramlette and Eugene E. Bouchard. The authors discuss
optimizing aircraft designs when the task is posed as that of optimizing a list of parameters.
They have approached the problem with a number of optimization algorithms, including a genetic
algorithm using real number representation. They also discuss the performance of each algorithm
and describe some innovative techniques used in their quite successful genetic algorithm,
including the technique of generating a large number of initial population members and then
working only with the best ones.
Genetic Algorithms in Parametric
Design of Aircraft, by Mark F. Bramlette and Eugene E. Bouchard. The authors discuss
optimizing aircraft designs when the task is posed as that of optimizing a list of parameters.
They have approached the problem with a number of optimization algorithms, including a genetic
algorithm using real number representation. They also discuss the performance of each algorithm
and describe some innovative techniques used in their quite successful genetic algorithm,
including the technique of generating a large number of initial population members and then
working only with the best ones.
 m, where m is the number of nodes), and a solution by an ordered sequence of
such segments. This encoding has many problems.
m, where m is the number of nodes), and a solution by an ordered sequence of
such segments. This encoding has many problems. Path encoding is the most intuitive one:
every node is assigned a number (e.g. from 0 up to n-1) and solutions are represented
by the ordered sequence of visited nodes.
Path encoding is the most intuitive one:
every node is assigned a number (e.g. from 0 up to n-1) and solutions are represented
by the ordered sequence of visited nodes. Partially-Mapped Crossover or PMX
Partially-Mapped Crossover or PMX