IV.
|
MODELS FOR THE PARALLELIZATION OF
GENETIC ALGORITHMS
|
Contents of this chapter
-
IV.1 Need of Parallelization
-
IV.2 Fine and Coarse Grain Models
-
IV.3 A Global Vision of the Existing Parallel GA Software
-
IV.4 Object Orientation and Parallelism
-
IV.3 Applications and Relationships with the Sequential Models
IV.1 Need of Parallelization
Sequential GAs have many succesfull applications to very different domains
but there exists a number of drawbacks in their utilization, namely:
In order to solve these shortcomings and also in order to study new models
of higher efficiency and efficacy, parallel models of GAs and in general
of EAs have been devised and used. Parallel GAs are not only an extension
of the traditional GA sequential model but they represent a new class of
algorithms in that they make a different search work. Thus we do not only
expect a Parallel Genetic Algorithm (PGA) to be more
efficient but also to need a smaller number of evaluations of the target
function.
Many different approaches to PGAs exist and they differ in many aspects.
It follows one possible classification of parallel GAs attending to three
concepts: the parallel model, the distribution of the population and the
implementation. This is not the sole classification one can made for PGAs
because it is very normal that the existing PGAs combine several caracteristics
from these apparently disjoin models.
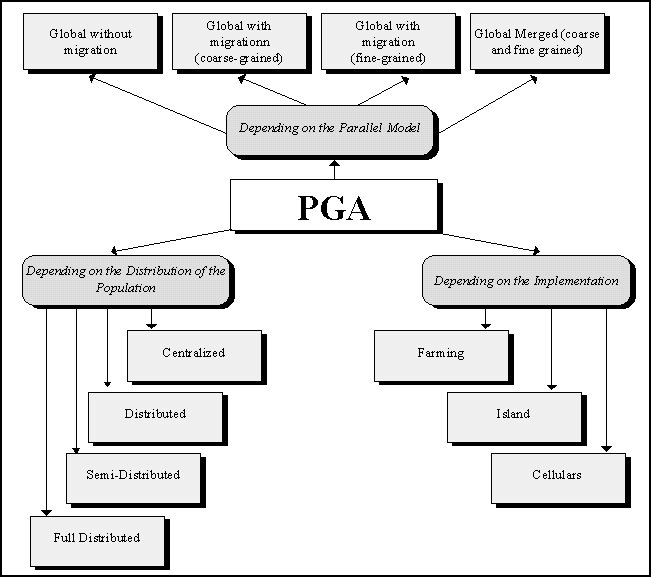
Figure 1. One Possible Classification of Parallel GAs.
IV.2 Fine and Coarse Grain Models
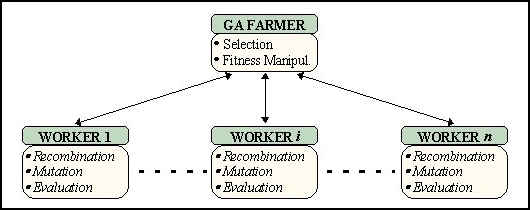
In the beginning of the parallelization of these algorithms the well-known
farming method was used. In this way a central processor performs
the selection operations while the associated slave processors perform
the recombination, mutation and the evaluation of the fitness function.
The last operation (evaluation) usually represent the most time-consuming
load of the genetic algorithm.
 However, One of the most accepted classification for parallel GAs divide
them attending to their parallel grain, that is, the relationship between
computation and communication. Thus we can distinguish among coarse
and fine grain models.
However, One of the most accepted classification for parallel GAs divide
them attending to their parallel grain, that is, the relationship between
computation and communication. Thus we can distinguish among coarse
and fine grain models.
Typical coarse grain models consist in a set of parallel subpopulations
that evolve independently from each other and that periodically exchange
individuals among them. The topology for the exchanges is usually a ring
or else some similar disposition. The subpopulations undergo exactly the
same genetic operations on the same kind of genotype and the result is
the best individual found in the overall population.
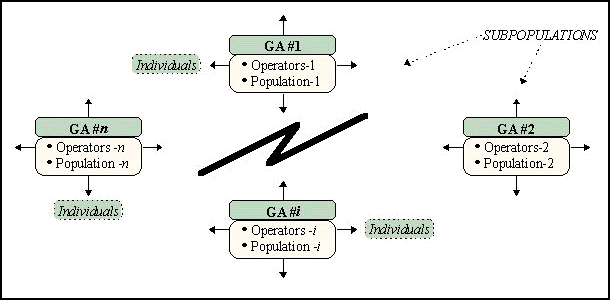
Figure 3. A Distributed (Migration) GA.
When dealing with a distributed GA some additional parameters need to be
defined. If migration of individuals has to take place then the rate
for the migrations and the number of individuals to migrate come
into scene. We also need to decide which individuals are going to migrate.
Finally the decision on the target subpopulation determines the global
topology of the distributed system. Traditionally, the topology is a ring,
one individual -the best or a random individual- migrates in every migration
step and migrations take place at some predefined and periodic moments
(althought some criteria for more controlled migrations have been considered
in this field, usually performing migrations when some condition holds
-the standard deviation falls below a given bottom limit, etc...-).
The migration scheme is very suited for a implementation in a network
of workstations. The existing UNIX networks with TCP/IP communication protocols
are the preferred for many researchers due to its relatively easy used
and also to the existence of many communication tools: socket interface,
PVM, etc...
On the other hand cellular (also known as massively parallel
GAs) genetic algorithms use a spatial disposition for the individuals of
one single population. Genetic operations take place in parallel for every
node of the population but every individual interacts only with its neighborhood.
Hence the selection, crossover and mutation take place by only considering
the adjacent strings. The replacement policy destroys the considered individual
by overwriting it with the newly computed string.
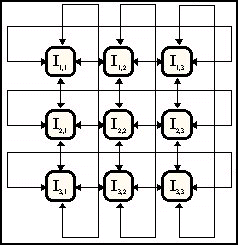
Figure 4. A Massively Parallel (Cellular) GA.
Cellular GAs have been implemented on multiprocessors due to the close
similarities between the model and the physical disposition of CPUs. OCCAM
and different versions of C have been used in the implementation. At present,
multiprocessors machines like Transputers are being shifted to applications
in which we need to execute a sequential algorithm with high speed. However
cellular GAs on multiprocessors are not very frequent because the parallel
market has plenty of local area network (cheaper, very fast, resources
sharing, ...). One intermediate approach could be the simulation of a fine-grained
GA in a network of workstations.
In cellular GAs, the isolation by distance property allows a high diversity
and the selection pressure is alse weaker due to the local selection operator.
The appearance of new species of solution in the grid (for example) and
the refinement of existing solutions are both allowed and desired. The
exploitation/exploration balance is then in many applications quite well
developed by a parallel cellular GA.
Figure 5. Evolution in a Parallel (Cellular) GA.
IV.3 A Global Vision of the Existing Parallel
GA Software
In this section we make a survey of the algorithms and software more readily
accessible in this area. Let us begin with a temporal review of parallel
GAs (PGAs). The most well-known cgpGAs and their main characteristics
sorted by date of referred appearance are:
TABLE I. OVERVIEW OF PARALLEL GAs BY YEAR
|
cgpGA
|
Ref.
|
Year
|
Main Characteristics
|
| PGA |
[55]
|
1987
|
Generational cgpGA on an Intel
iPSC hypercube (8 CPUs). Migrate the best. Dynamic Top. |
| dGA |
[68]
|
1989
|
Distributed populations. Good
results with 20% of population migrants every 20 generats. |
| GENITOR II |
[73]
|
1990
|
Steady-State islands with ranked
selection and reduced surrogate crossover |
| PGA |
[51]
|
1991
|
Sub-populations in a circular
ladder-like 2-D topology. Migrate the best, local hill-climbing |
| SGA-cube |
[23]
|
1991
|
Made for nCUBE2. This is the parallel
extension of the well known simple GA of Goldberg |
| PARAGENESIS |
---
|
1992
|
Made for the CM-200. This places
one individual in every CPU |
| PeGAsuS |
[59]
|
1993
|
Targeted for MIMD machines and
written in a very high and flexible description language |
| GAMAS |
[56]
|
1994
|
Uses 4 very heterogeneous species
(islands) and quite specialized migrations and genotyp. |
| iiGA |
[44]
|
1994
|
Injection island GA with hierarchical
heterogeneous nodes and asynchronous migrations |
| SP1-GA |
[42]
|
1994
|
128 steady-state islands on an
IBM SP1 machine of 128 nodes. 2-D toroidal mesh. mr=1 |
| DGENESIS |
[47]
|
1994
|
Free topology, migration and policies
for selection. Implemented with sockets and UDP |
| GALOPPS |
[30]
|
1996
|
Very flexible. Implemented with
PVM and comprising a large number of operators |
| GDGA |
[45]
|
1996
|
Synchronous. Simulated on one
processor. Generational. Fuzzy crossover and FP genes |
| CoPDEB |
[2]
|
1996
|
Every island uses its own probabilities
for mutation & crossover and specialized operators |
Of course this list is not complete, but it gives us a feeling of the
evolution of cgpGAs over recent years. We will
offer more details about these and other algorithms in the following
tables.
There has been a tendency towards making PGAs that run on clusters of
machines paying a great attention to
their portability. Old systems like transputer machines do not support
recent implementations. Also, new
developments in JAVA are appearing as a confirmation of these tendencies.
In order to complete our historical and application overview we give
an original classification of sequential and parallel GAs into three
major categories [59] according to their specific objectives:
· Application Oriented: These
are black-box systems designed to hide the details of GAs and help the
user in developing applications for specific domains. Some of these are
useful for different purposes such as scheduling or telecommunications
(e.g. PC/BEAGLE). Some others are much more application oriented (like
OMEGA for finance). Usually they are menu-driven and easily parameterizable.
· Algorithm Oriented: Based
on specific algorithms. The source code is available in order to provide
their easy incorporation into new applications. This class may be further
sub-divided into:
· Tool Kits: These are flexible
environments for programming a range of different GAs and applications.
They can be sub-divided into:
We present some detailed tables with a classification of algorithms, and
mark this classification with the above labels. Also, we use the PROP
label for distinguishing between commercial and proprietary systems. We
have also opened the contents of this table to non-cgpGAs to offer a better
view of the global achievements of this class of evolutionary algorithms.
See the following tables.
TABLE II. OVERVIEW OF SOME UP-TO-DATE EXISTING SEQUENTIAL
AND PARALLEL GENETIC ALGORITHMS
|
Genetic Algorithm
|
Ref.
|
Lang.
|
OS/Machine
|
Kind of GA
|
Algorithm
|
Seq/Par
|
Evolution
|
HOW TO GET IT!
|
|
ASPARAGOS
|
[32]
|
C
|
64 T800 transp
|
Algorithm Specific
|
Single / No pop.
|
PAR
|
Local
|
---
|
|
CoPDEB
|
[2]
|
C
|
UNIX
|
Algorithm Specific
|
Single / No prop.
|
PAR
|
Gen.
|
adamidis@it.teithe.gr
|
|
DGENESIS 1.0
|
[47]
|
C
|
UNIX
|
Algorithm Specific
|
Single / No Prop.
|
PAR
|
Percentage
|
ftp.aic.nrl.navy.mil
|
|
ECO-GA
|
[21]
|
C?
|
UNIX?
|
Algorithm Specific
|
Single / No Prop.
|
PAR
|
Local
|
yuval@wisdom.weizmann.ac.il
|
|
EM 2.1
|
[69]
|
C
|
DOS
|
Algorithm Library
|
Algrthm. Library
|
SEQ
|
Gen. / S. S.
|
[130.149.192.50]/W
|
|
EnGENEer
|
[60]
|
C
|
UNIX
|
General Purpose
|
Algrthm. Library
|
SEQ/par
|
Gen. / S. S.
|
---
|
|
ESCAPADE 1.2
|
[35]
|
---
|
---
|
Algorithm Specific
|
Single / No Prop.
|
---
|
E. S.
|
ls11.informatik.uni-dortmund.de
|
|
EVOLVER 2.0
|
---
|
C++
|
DOS & MAC
|
Application Orient.
|
Single / Prop.
|
SEQ
|
---
|
Axcélis (used in a spread sheet)
|
|
GA Workbench
|
[37]
|
C
|
DOS
|
Educational
|
Algrthm. Library
|
SEQ
|
Percentage
|
camcon.co.uk
|
|
GAGA
|
[8]
|
C
|
UNIX
|
Algorithm Specific
|
Single / No Prop.
|
SEQ
|
---
|
cs.ucl.ac.uk/darpa/gaga.shar
|
|
GAGS
|
[48]
|
C++
|
UNIX & DOS
|
General Purpose
|
Algrthm. Library
|
SEQ
|
Gen.
|
http://kal-el.ugr.es/GAGS
|
|
GAlib
|
[71]
|
C++
|
UNIX
|
Algorithm Specific
|
Algrthm. Library
|
SEQ
|
Gen.
|
lancet.mit.edu/pub/ga/galib242.tar.gz
|
|
GALOPPS 3.1
|
[30]
|
C
|
UNIX & DOS
|
Algorithm Specific
|
Single / No Prop.
|
PAR
|
Gen.
|
isl.msu.edu/pub/GA
|
|
GAMAS
|
[56]
|
C?
|
UNIX
|
Algorithm Specific
|
Single / No Prop
|
PAR
|
Gen.
|
---
|
|
GAME
|
[66]
|
C++
|
UNIX & DOS
|
General Purpose
|
Algrthm. Library
|
SEQ/par
|
Gen. / S. S.
|
bells.cs.ucl.ac.uk/papagena/game
|
|
GAucsd 1.2 / 1.4
|
[61]
|
C
|
UNIX, DOS ...
|
Algorithm Specific
|
Single / No Prop.
|
SEQ
|
Gen.
|
http://www.aic.nrl.navy.mil/galist/src/GAucsd14.sh.Z
|
|
GDGA
|
[45]
|
C
|
UNIX
|
Algorithm Specific
|
Single / No Prop.
|
SEQ/par
|
Gen.
|
lozano@decsai.ugr.es
|
|
GENESIS 5.0
|
[33]
|
C
|
UNIX, DOS ...
|
Algorithm Specific
|
Single / No Prop.
|
SEQ
|
Percentage
|
http://www.aic.nrl.navy.mil/galist/src/genesis.tar.Z
|
|
GENEsYs 1.0
|
---
|
C
|
UNIX
|
Algorithm Specific
|
Single / No Prop.
|
SEQ
|
Percentage
|
[129.217.36.140]/pub/GA/src/GENEsYs-1.0.tar.Z
|
|
GENITOR I - II
|
[73]
|
C
|
UNIX
|
Algorithm Specific
|
Single / No Prop.
|
SEQ-PAR
|
S. S. / Rank
|
*/genitor
|
|
HSDGA
|
[70]
|
C
|
HELIOS
|
Algorithm Specific
|
Single / No Prop.
|
PAR
|
Local
|
---
|
|
LibGA
|
[18]
|
C
|
UNIX
|
Algorithm Specific
|
Single / No Prop.
|
SEQ
|
Gen. / S. S.
|
*/libga
|
|
OMEGA
|
[66]
|
---
|
---
|
Application Orient.
|
Prop.
|
SEQ
|
---
|
KiQ Limited (used in business applications)
|
|
OOGA
|
[22]
|
CLOS
|
any LISP
|
Algorithm Library
|
No Prop.
|
SEQ
|
Gen. / S. S.
|
TSP, P.O. Box 991, Melrose, MA 02176-USA
|
|
PARAGENESIS
|
---
|
C*
|
CM-200
|
Algorithm Specific
|
Single / No Prop
|
PAR
|
Percentage
|
[192.26.18.74]/pub/galist/src/ga/paragenesis.tar.Z
|
|
PC/BEAGLE
|
[59]
|
---
|
DOS
|
Application Orient.
|
Prop.
|
SEQ
|
S. S.
|
Pathway Research Ltd. (used in machine learning)
|
|
PeGAsuS
|
[59]
|
C
|
UNIX, ...
|
General Purpose
|
Algrthm. Library
|
PAR
|
Gen. / S. S.
|
---
|
|
PGA 2.5
|
---
|
C
|
UNIX & DOS
|
Algorithm Specific
|
Single / No Prop
|
PAR
|
Gen.?
|
http://www.aic.nrl.navy.mil/galist/src
/pga-2.5.tar.Z
|
|
PGAPack
|
[43]
|
C
|
UNIX, ...
|
Algorithm Library
|
Algrthm. Library
|
PAR
|
Gen. / S. S.
|
http://www.mcs.anl.gov/pgapack.html
|
|
RPL2
|
[57]
|
C
|
UNIX, ...
|
General Purpose
|
Prop. Library
|
PAR
|
Gen. / S. S.
|
http://www.quadstone.co.uk/~rpl2
|
|
SGA
|
[26]
|
C
|
UNIX
|
Algorithm Specific
|
Single / No Prop
|
SEQ
|
Gen.
|
[192.26.18.56] ...
sgac_94m.tgz
|
|
SGA-Cube
|
[23]
|
C
|
nCUBE 2
|
Algorithm Specific
|
Single / No Prop
|
PAR
|
Gen.
|
[192.26.18.56] ...
sgacub94.tgz
|
|
SPLICER 1.0
|
[54]
|
C
|
UNIX & MAC
|
General Purpose
|
Algrthm. Library
|
SEQ
|
Gen.
|
galileo.jsc.nasa.gov
|
|
SUGAL 2.0
|
[38]
|
C
|
UNIX, DOS, ...
|
Algorithm Library
|
Algrthm. Library
|
SEQ
|
Gen. / S. S.
|
http://osiris.sund.ac.uk/ahu/sugal/home.html
|
|
TOLKIEN
|
---
|
C++
|
UNIX
|
General Purpose
|
Algrthm. Library
|
SEQ
|
Gen.?
|
*/tolkien
|
|
XpertRule GenAsys
|
---
|
---
|
---
|
Application Orient.
|
Prop.
|
SEQ
|
---
|
Attar Software (used in design and scheduling)
|
TABLE III. MEANING OF THE SYMBOLS IN TABLE II
|
Symbol
|
Meaning of the Symbol
|
| Local |
The algorithm performs operations
on every string by interactions with only its neighboring strings |
| Gen. |
Generational: The basic algorithmic
step is a full generation of individuals |
| S. S. |
Steady-State: the basic algorithmic
step is the computation of a very low number of individuals (usually one) |
| Percentage |
GAP: The algorithm works and replaces
only a given percentage of the whole population of individuals |
| Rank |
The individuals are sorted according
to increasing fitness and the selection uses the Ďpositioní in the rank
(and not the fitness itself) |
| par |
Parallel version is not available
yet |
| SEQ/PAR |
The algorithm is able to work
either in sequential and in parallel |
| * |
http://www.cs.cmu.edu/afs/cs/project/ai-repository/ai/areas/genetic/ga/systems |
| W |
pub/software/Evolution_Machine/em_tc.exe |
TABLE IV. CLASSIFICATION OF THE GENETIC SYSTEMS
|
Application
|
Algorithm Oriented
|
Tool Kits
|
|
Oriented
|
Algorithm Specific
|
Algorithm Libraries
|
Educational
|
General Purpose
|
| |
ASPARAGOS
|
|
|
|
| |
CoPDEB
|
EM 2.1
|
|
|
|
EVOLVER 2.0
|
DGENESIS 1.0
|
|
|
EnGENEer
|
| |
ECO-GA
|
|
|
|
| |
ESCAPADE 1.2
|
|
|
GAGS
|
| |
GAGA
|
OOGA
|
|
|
| |
GAlib
|
|
|
GAME
|
|
OMEGA
|
GALOPPS 3.1
|
|
|
|
| |
GAMAS
|
|
|
PeGAsuS
|
| |
GAucsd 1.2 / 1.4
|
|
GA Workbench
|
|
| |
GDGA
|
PGAPack
|
|
RPL2
|
| |
GENESIS 5.0 - GENEsYs 1.0
|
|
|
|
|
PC/BEAGLE
|
GENITOR I Y II
|
|
|
Splicer 1.0
|
| |
HSDGA
|
|
|
|
| |
libGA
|
|
|
TOLKIEN
|
| |
PGA 2.5
|
SUGAL 2.0
|
|
|
| |
PARAGENESIS
|
|
|
|
|
XpertRule GenAsys
|
SGA
|
|
|
|
| |
SGA-Cube
|
|
|
|
TABLE V. DETAILS OF THE PARALLEL GAs
|
Parallel GA
|
Kind of Parallelism
|
Topology
|
Present Applications
|
|
ASPARAGOS
|
Fine grain. Applies Hill-Climbing if no improvement |
Ladder |
TSP |
|
CoPDEB
|
Coarse grain. Every sub-pop. applies different
operators |
Full Connected |
Func. Opt. and ANNís |
|
DGENESIS 1.0
|
Coarse grain with migrations among sub-populations |
Any Desired |
Function Optimization |
|
ECO-GA
|
Fine grain. One of the first of its class |
Grid |
Function Optimization |
|
EnGENEer
|
Global parallelization (parallel evaluations) |
Master / Slave |
Very Different |
|
GALOPPS 3.1
|
Coarse grain. A very portable software |
Any Desired |
Func. Opt. and Transport |
|
GAMAS
|
Coarse grain. Uses 4 species of strings (nodes) |
Fixed Hierarchy |
ANN, Func. Opt., ... |
|
GAME
|
Parallel version not available yet. Object Oriented |
Any Desired |
TSP, Func. Opt., ... |
|
GDGA
|
Coarse Grain. Admits explicit exploration/exploitation |
Hypercube |
Func. Opt. (floating p.) |
|
GENITOR II
|
Coarse grain. Interesting crossover operator |
Ring |
Func. Opt. and ANNís |
|
HSDGA
|
Hierarchical coarse and fine grain GA. Uses
E. S. |
Ring, Tree, Star, ... |
Function Optimization |
|
PARAGENESIS
|
Coarse grain. Made for the CM-200 (1 ind. -
1 CPU) |
Multiple |
Function Optimization |
|
PeGAsuS
|
Coarse or fine grain. High-level programming.
MIMD |
Multiple |
Teaching and Func. Opt. |
|
PGA 2.5
|
Coarse grain. Makes migrations among sub-populations |
Multiple |
Knapsack and Func. Opt. |
|
PGAPack
|
Global parallelization (parallel evaluations) |
Master / Slave |
Function Optimization |
|
RPL2
|
Coarse grain. Very flexible and open to new
models |
Any Desired |
Research and Business |
|
SGA-Cube
|
Coarse Grain. Made for the nCUBE 2 |
Hypercube |
Function Optimization |
IV.4 Object Orientation and Parallelism
(Alba, Troya, 1997)
Traditional imperative languages like C or PASCAL endow the implementation
with a high computational speed. However, more actual technologies such
as object oriented design can have an outstanding impact on the quality
of the implementation. Among the benefits of using the OO methodology for
a PGA implementation, the following ones can be mentioned:
-
Reusing the software is at present difficult: a software tool is either
too specific and thus useless for other problems or it is too general and
thus inefficient. OO can help in reusing software, in the fast building
of prototypes and also in the security of this software.
-
A common architecture of classes for a genetic system could be created
and enriched by different people and experience. Comparisons should then
be readily simple and meaningful.
An object oriented implementation of a PGA can also help experimenting
and combining different granularities, topologies, operators, hybridization,
competition or cooperation with other techniques and offers many other
added facilities to create new models of evolution.
Two actual implementations that follow the OO methodology in C++ are
described in this section. We call them dGANN and dGAME. The high parameterization
of parallel GAs, their combinations, comparisons and development have been
largely enhanced by using the OO design. We discuss a general methodology
for building a parallel GA system with high flexibility and then present
the two mentioned actual models.
IV.4.1 PGA Models and OO Implementation
This section discusses the architecture of a PGA. For that purpose, some
ideas on parallel models and the use of object orientation are presented.
From an algorithmic point of view, useful existing techniques must be
examined for inclusion in the PGA. Hybridization and theoretical background
are needed to improve existing models or proposing new PGAs.
The figure below represents the elements we should consider when developing
an OO parallel GA (or EA).
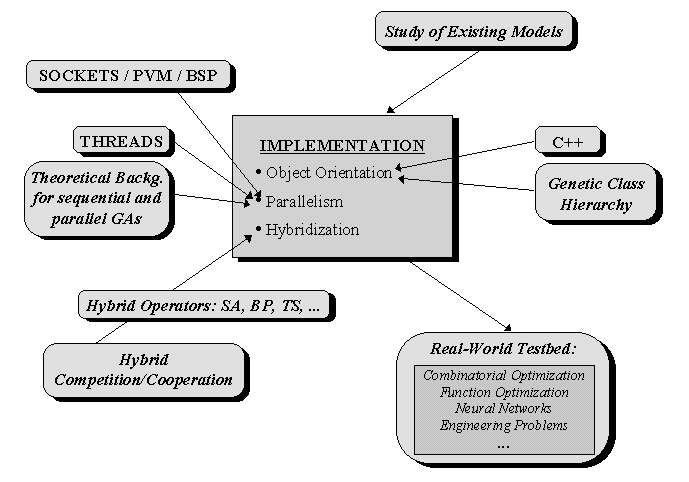 Figure 6. Proposal of working environment for a PGA software
system.
Figure 6. Proposal of working environment for a PGA software
system.
Two mixed levels are shown in the figure. The design level is related
to the study of existing approaches, the concrete parallel model, how to
perform hybridization and the need of evaluating the PGA on a real-world
testbed.
On the other hand, the implementation level is related to internal details
of the system. We propose an object oriented design for several reasons
we will justify later in this section. The way of achieving parallelism
is also important for the resulting PGA system.
We strongly believe that any parallel model should help to efficiently
solve real complex problems. You can use almost any sequential or parallel
system for the study of theoretical issues, but both efficiency and multiple
ways of expressing one or more parallel models are required for addressing
real problems . Changing or adding operators (static or dynamically during
the search) should be made in a structured (and not in a problem-dependent)
form.
Parallel algorithms do not usually run in massively parallel computers
since LANs are much more popular. Some present types of LAN technologies
as Fast Ethernet or ATM make communication delays as small as hard disk
accesses. Hence massive parallelism should be simulated in the local network
(Maruyama, Hirose, Konagaya, 1993).
When simulating parallelism in one processor you must choose between
having a process that encapsulates the parallel model directly or using
threads (if possible, kernel threads). Sometimes a model could work as
different UNIX processes running in the same machine, but might become
very inefficient in a distributed environment.
IV.4.2 The Benefits of Using an OO Design
The traditional aspect of a GA (see figure 7) can drastically change by
means of an OO design and implementation.
 Figure 7. Traditional imperative pseudocode of a GA.
Figure 7. Traditional imperative pseudocode of a GA.
 Figure 8. The shape and semantics of this GA differ from
implementations built with imperative languages. For example, explicit
initialization of the GA could be helpful for controlling its execution
in a parallel platform.
Figure 8. The shape and semantics of this GA differ from
implementations built with imperative languages. For example, explicit
initialization of the GA could be helpful for controlling its execution
in a parallel platform.
With practically the same amount of effort we can both specify an imperative
pseudocode or else a concrete-working code for a problem in terms of object
orientation. The last solution is much more flexible and rich in the data
structures it uses and also in the performed operations (as well as in
future extensions to other problems).
Object orientation is not just a new style for implementations. It represents
a new form of conceiving the design of a software tool.
Thus, not only we can express in a new manner a PGA but we can also
add new features such as new schemes of evolution, genotypes, lists of
operators, parallel models and parameters in almost a straightforward way.
IV.4.3 The Two Proposed Systems
In this subsection we want to propose two separated systems that incorporate
the main ideas we outlined in the previous sections on PGAs and OO.
In order to create objects suited for structured addition of operators
you need to completely separate the class of individuals and the
class of the operator pool. The operator pool is a list of operators
that can dynamically accept or reject new operators, and of course change
their list of parameters. The idea of an ordered list of operators to be
applied each one with its own list of parameters (and not just its application
rate) can be very helpful in controlling and enhancing the PGA performance.
The individuals also must be separated from their contents in the sense
that the kind of genotype must be a different class in order to allow an
independent manipulation. Hence a problem class must exist to separate
the full software system from the actual problem we are trying to solve
with it.
Finally we need communication classes for transferring data among processors
and we need also some classes for expressing parallel interactions among
GAs. A central monitor is normally needed in order to deal with the user
(get global and particular statistics and status, kill a process, save
and load populations on line, etc...). In some models it should be interesting
the central monitor to make also algorithmic work for the PGA.
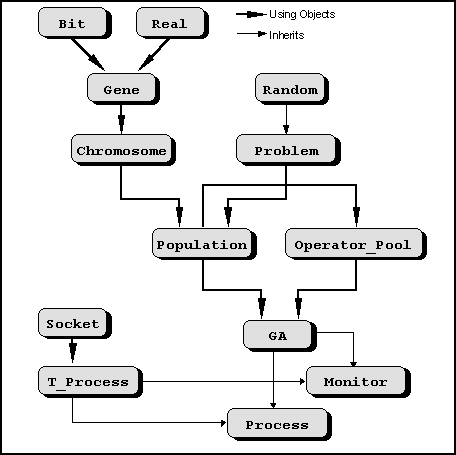 Figure 9. Proposal of a hierarchy of dGA classes (dGANN).
Figure 9. Proposal of a hierarchy of dGA classes (dGANN).
Figure 9 shows the class hierarchy for the dGA system we call dGANN.
This proposal deals with fault tolerance in the sense that if a genetic
process dies the system is able to keep on running. We propose asynchronous
exchanges of information (like in (Gorges,
1989) or (Munetomo, 1993)),
because this will ease the fault tolerance aspect (synchronous communication
would be too slow).
A socket interface has been initially considered the faster and more
compatible way of implementing a distributed PGA. Classes for exchanging
messages are needed and also for controlling the integrity of the system
during execution. New genotypes can be easily added to this class hierarchy.
In order to have a good general parallel model we think that the implementation
could take into account (of course the experience of other existing models
and) the benefits of using C++. You can use another OO languages as Eiffel,
Ada or Smalltalk but C++ is the most widely accepted.
Despite its advantages, C++ do not provide parallel support. Thus if
we want to parallelize an OO model we need some kind of communication services
for the implementation. Parallelization is specially easy and flexible
with OO.
The drawback is that cellular GAs cannot be easily derived from this
hierarchy since the object that represents one individual should run in
parallel with the rest.
Cellular GAs (or mpGAs) have many points in common with distributed
GAs (dGAs):
-
They both use some kind of spatial topology: dGAs usually a ring and mpGAs
usually locate individuals in a grid.
-
They both make parallel exchanges of information among neighbors (neighbors
are subpopulations of N individuals in dGAs or else just single individuals
in mpGAs).
-
The individuals of a traditional population can be viewed as a full-connected
cellular topology.
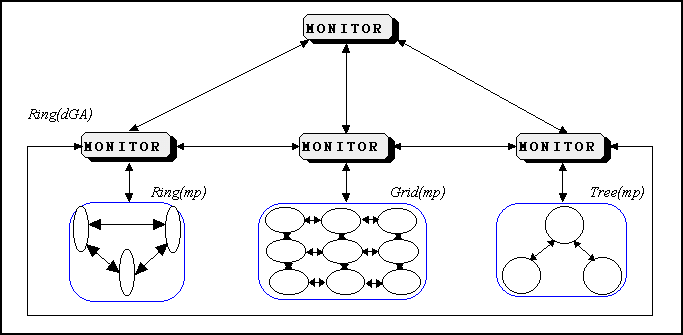 Figure 10. The dGAME model. Merging of models can yield
more robust searches. There exist two levels of search: a dGA of mpGAs.
Figure 10. The dGAME model. Merging of models can yield
more robust searches. There exist two levels of search: a dGA of mpGAs.
In the above example the low monitors exchange individuals in a ring
topology (much like a migration dGA scheme). Each L-monitor
controls a population with a given cellular (mpGA) disposition of individuals.
With these considerations we are ready to think in a unified parallel
model that can be implemented in the same software system and that additionally
opens new questions relating the merging and cooperation among different
submodels. This is good if we can capture in a given parallel model the
advantages of the combined submodels (trying to minimize their associated
drawbacks). Our dGAME extension of the GAME (Stender,
1993) environment is the first step in this sense.
Besides these new ideas, cooperation or competition among different
kind of GAs or even different algorithms can be achieved. Such an OO distributed
GA could deal with most of requirements of existing problems.
Most of these concepts can be found in our dGAME environment. An OO
design, combinations of topologies and merging of arbitrary dGA-mpGA models
are the more important characteristics of dGAME.
IV.5 Applications and Relationships with the Sequential
Models
From a different point of view we present in table IV a set of representative
applications of PGAs in order to
show the wide spectrum of their successful applications (i. e. robustness).
TABLE VI. SOME APPLICATIONS OF PARALLEL GAs
|
Reference
|
Application Domain
|
|
[7]
|
Parallel training of artificial
neural networks. Hybridized and pure cgpGAs |
|
[19]
|
Synthesis of VLSI circuits |
|
[31]
|
Function optimization |
|
[42]
|
Set partitioning problem |
|
[44]
|
Graph partitioning problem |
|
[49]
|
Constraint Optimization, reordering
problems, ... |
|
[51]
|
Traveling salesperson problem
(TSP), function optimization |
|
[53]
|
Distributing the computing load
onto a set of processing nodes |
|
[56]
|
The file allocation problem, XOR
neural network, sine envelope sine wave function |
|
[66]
|
Systems modelling, protein tertiary
structure prediction and two-dimensional bin packing problems |
|
[68]
|
Walsh polynomials |
|
[73]
|
Optimization of the connection
weights of neural networks (XOR, bin-adder, ...) and function optimization |
There exist many other applications in very interesting domains such
as frequency assignment problems, market
predictions, game theory, filters, graphic transformations, etc. Some
of these applications motivated the need for
new classes of genotypes that can be thought of consisting in strings
of arbitrary symbols. A further extension led to the mentioned genetic
programming paradigm [40] in which the individuals
are trees of symbols representing computer programs, fuzzy controllers,
or many other kinds of high-level concepts. This is a new and important
research area in
which PGAs are developing quickly. Also new genotypes and operators
are being developed for dealing with
constraint problems and combinatorial optimization.
Besides that, the importance of parallel and distributed GAs is growing
due to recent studies in which no parallel
hardware is needed but still the search is enhanced due to neighborhoods
similar to [32], [46] or [51].
References
-
P. Adamidis. "Review of Parallel Genetic Algorithms Bibliography".
Internal T.R., Aristotle University of Thessaloniki, November (http://www.control,ee.auth.gr/~panos/papers/pga_review.ps.gz).
1994.
-
P. Adamidis, V. Petridis. "Co-operating Populations with
Different Evolution Behavior". Proceedings of the Second IEEE Conference
on Evolutionary Computation, pp 188-191. 1996.
-
E. Alba, J. F. Aldana, J. M. Troya. "Load Balancing and
Query Optimization in Dataflow Parallel Evaluation of Datalog Programs".
Proceedings of the International Conference on Parallel and Distributed
Systems, Lionel M. Ni (ed.). IEEE Computer Society Press, pp 682-688.
1994.
-
E. Alba, J. F. Aldana, J. M. Troya. "A Genetic Algorithm
for Load Balancing in Parallel Query Evaluation for Deductive Relational
Databases". Procs. of the I. C. on ANNs and GAs, D.W. Pearson, N.C.
Steele, R.F. Albrecht (eds.), pp 479-482. Springer-Verlag. 1995.
-
E. Alba, C. Cotta, J. M. Troya. "Type-Constrained Genetic
Programming for Rule-Base Definition in Fuzzy Logic Controllers". Proceedings
of the First Annual Conference on Genetic Programming, J. R. Koza,
D. E. Goldberg, D. B. Fogel & R. L. Riolo (eds.), Stanford Univ., Cambridge,
MA. The MIT Press, pp 255-260. 1996.
-
E. Alba, J. M. Troya. "Genetic Algorithms for Protocol
Validation". Proceedings of the PPSN IV I.C., H. M. Voigt, W. Ebeling,
I. Rechenberg & H. P. Schwefel (eds.), Berlin. Springer-Verlag, pp
870-879. 1996.
-
E. Alba, C. Cotta. "Evolution of Complex Data Structures".
Informática y Automática, 30(3), pp 42-60. September,
1997.
-
C. Alippi, P. Treleaven. "GAME: A Genetic Algorithms
Manipulation Environment". Internal Report Department of Computer Science,
UCL. 1991.
-
J. Antonisse. "A New Interpretation of Schema Notion
that Overturns the Binary Encoding Constraint". Proceedings of the 3rd
ICGA, J. D. Schaffer (ed.), Morgan Kaufmann, pp 86-91. 1989.
-
T.Bäck, D. Fogel, Z. Michalewicz (eds.) Handbook
of Evolutionary Computation (Oxford University Press). 1997.
-
T. Bäck, H. P. Schwefel. "An Overview of Evolutionary
Algorithms for Parameter Optimization". Evolutionary Computation,
1 (1), pp 1-23, The MIT Press. 1993.
-
J. E. Baker. "Adaptive Selection Methods for Genetic
Algorithms". Proceedings of the First International Conference on Genetic
Algorithms and Their Applications, J. J. Grefenstette (ed.), Lawrence
Erlbaum Associates, Publishers, pp 101-111. 1985.
-
J. E. Baker. "Reducing Bias and Inefficiency in the
Selection Algorithm". Proceedings of the Second International Conference
on Genetic Algorithms, J. J. Grefenstette (ed.), Lawrence Erlbaum Associates,
Publishers, pp 14-21. 1987.
-
T. C. Belding. "The Distributed Genetic Algorithm Revisited".
Proceedings of the 6th International Conference on GAs, L. J. Eshelman
(ed.), Morgan Kaufmann, pp 122-129. 1995.
-
E. Cantú-Paz. "Parallel Genetic Algorithms in
Distributed Memory Architectures". Master Thesis Dissertation, Instituto
Tecnológico Autónomo de México. May 1994.
-
E. Cantú-Paz. "A Summary of Research on Parallel
Genetic Algorithms". R. 95007, July 1995. Also revised version,
IlliGAL R. 97003. May 1997.
-
A. Chipperfield, P. Fleming. "Parallel Genetic Algorithms".
Parallel and Distributed Computing Handbook, A. Y. H. Zomaya (ed.),
MacGraw-Hill , pp 1118-1143. 1996.
-
A. L. Corcoran, R. L. Wainwright. "LibGA: A User-Friendly
Workbench for Order-Based Genetic Algorithm Research". Proceedings of
the 1993 ACM/SIGAPP Symposium on Applied Computing, ACM Press. 1993.
-
F. Corno, P. Prinetto, M. Rebaudengo, M. Sonza-Reorda.
"Exploiting Competing Subpopulations for Automatic Generation of Test Sequences
for Digital Circuits". Procs. of the PPSN IV I.C., H. M. Voigt,
W. Ebeling, I. Rechenberg, H. P. Schwefel (eds.), Springer-Verlag, pp 792-800.
1996.
-
C. Cotta, E. Alba, J. M. Troya. "Evolutionary Design
of Fuzzy Logic Controllers". IEEE Catalog N. 96CH35855, Proceedings
of the ISISCí96 Conference, Dearborn, MI pp 127-132. 1996.
-
Y. Davidor. "A Naturally Occurring Niche & Species
Phenomenon: The Model and First Results". Procs. of the 4th ICGA,
R. K Belew, L. B. Booker (eds.), pp 257-263. 1991.
-
L. Davis, J. J. Grefenstette. "Concerning GENESIS and
OOGA". Handbook of Genetic Algorithms, L. Davis (ed.), New York:
Van Nostrand Reinhold, pp 374-376. 1991.
-
J. A. Erickson, R. E. Smith, D. E. Goldberg. "SGA-Cube,
A Simple Genetic Algorithm for nCUBE 2 Hypercube Parallel Computers". TCGA
Report No. 91005, The Univ. of Alabama. 1991.
-
L. J. Fogel, A. J. Owens, M. J. Walsh. Artificial
Intelligence Through Simulated Evolution. John Wiley, New York. 1966.
-
A. Geist, A. Beguelin, J. Dongarra, W. Jiang, R. Manchek,
V. Sunderam. PVM: Parallel Virtual Machine. A Usersí Guide and Tutorial
for Networked Parallel Computing. The MIT Press. 1994.
-
D. E. Goldberg. Genetic Algorithms in Search, Optimization
and Machine Learning; Addison-Wesley. 1989.
-
D. E. Goldberg. "Sizing Populations for Serial and Parallel
Genetic Algorithms". Proceedings of the 3rd ICGA, J. D. Schaffer
(ed.), Morgan Kaufmann, pp 70-79. 1989.
-
D. E. Goldberg, K. Deb, B. Korb. "Donít Worry, Be Messy".
Proceedings of the Fourth International Conference on Genetic Algorithms,
R. K. Belew and L. B. Booker (eds.), Morgan Kaufmann, San Mateo, CA, pp
24-30. 1991.
-
D. E. Goldberg, et al. "Critical Deme Size for Serial
and Parallel Genetic Algorithms". IlliGAL Report No. 95002. January
1995.
-
E. D. Goodman. An Introduction to GALOPPS v3.2. TR#96-07-01,
GARAGe, I. S. Lab., Dpt. of C. S. and C. C. C. A. E. M., Michigan State
University, East Lansing. 1996.
-
V. S. Gordon, D. Whitley. "Serial and Parallel Genetic
Algorithms as Function Optimizers". Procs. of the 5th ICGA, S. Forrest
(ed.), Morgan Kaufmann, pp 177-183. 1993.
-
M.Gorges-Schleuter. "ASPARAGOS An Asynchronous Parallel
Genetic Optimisation Strategy". Procs. of the 3rd ICGA, J. D. Schaffer
(ed.), Morgan Kaufmann, pp. 422-427. 1989.
-
J. J. Grefenstette. "GENESIS: A System for Using Genetic
Search Procedures". Proceedings of the 1984 Conference on Intelligent
Systems and Machines, pp. 161-165. 1984.
-
F. Herrera, M. Lozano, J. L. Verdegay. "Tackling Fuzzy
Genetic Algorithms". Genetic Algorithms in Engineering and Computer
Science, G. Winter, J. Périaux, M. Galán, P. Cuesta (eds.),
John Wiley & Sons, pp 167-189. 1995.
-
F. Hoffmeister. "The Userís Guide to ESCAPADE
1.2 A Runtime Environment for Evolution Strategies". Department of Computer
Science, University of Dortmund, Germany. 1991.
-
J. H. Holland. Adaptation in Natural and Artificial
Systems. Univ. of Michigan Press, Ann Arbor, MI. 1975.
-
M. Hughes. "Genetic Algorithm Workbench Documentation",
Cambridge Consultants Ltd. 1989.
-
A. Hunter. "Sugal Programming Manual v2.0". T. R.
in Univ. Sunderland, U.K.. July 1995.
-
B. A. Juslstrom. "What Have You Done for Me Lately?
Adapting Operator Probabilities in a Steady-State Genetic Algorithm". Proceedings
of the 6th International Conference on Genetic Algorithms, L. J. Eshelman
(ed.), Morgan Kaufmann, pp 81-87. 1995.
-
J. R. Koza. Genetic Programming.
The MIT Press. 1992.
-
T. Kuo, S. Y. Hwang. "A Genetic Algorithm with Disruptive
Selection". Proceedings of the 5th International Conference on GAs,
S. Forrest (ed.), Morgan Kaufmann, pp 65-69. 1993.
-
D. Levine. "A Parallel Genetic Algorithm fot the Set
Partitioning Problem". T. R. No. ANL-94/23, Argonne National Laboratory,
Mathematics and Computer Science Division. 1994.
-
D. Levine. "Users Guide to the PGAPack Parallel Genetic
Algorithm Library". T. R. ANL-95/18, January 31. 1996.
-
S. Lin, W. F. Punch and E. D. Goodman. "Coarse-Grain
Parallel Genetic Algorithms: Categorization and New Approach". Parallel
& Distributed Processing. October 1994.
-
M. Lozano. "Application of Fuzzy Logic Based Techniques
for Improving the Behavior of GAs with Floating Point Encoding". Ph.D.
Th., Dpt. of C. S. and A.I., Univ. Granada. July 1996.
-
B. Manderick, P. Spiessens. "Fine-Grained Parallel
Genetic Algorithms". Procs. of the 3rd I. C. on Genetic Algorithms,
J. D. Schaffer (ed.), Morgan Kaufmann, pp 428- 433. 1989.
-
M. Mejía-Olvera, E. Cantú-Paz. "DGENESIS-Software
for the Execution of Distributed Genetic Algorithms". Proceedings of
the XX Conferencia Latinoamericana de Informática, pp 935-946,
Monterrey, México. 1994.
-
J. J. Merelo, A. Prieto. GAGS, "A Flexible Object-Oriented
Library for Evolutionary Computation". Procs. of MALFO, D. Borrajo,
P. Isasi (eds.), pp 99-105. 1996.
-
Z. Michalewicz. Genetic Algorithms + Data Structures
= Evolution Programs. Springer-Verlag. 1992.
-
H. Mühlenbein. "Evolution in Time and Space - The
Parallel Genetic Algorithm". Foundations of Genetic Algorithms,
G. J. E. Rawlins (ed.), Morgan Kaufmann, pp 316-337. 1991.
-
H. Mühlenbein, M. Schomisch, J. Born. "The Parallel
Genetic Algorithm as Function Optimizer". Parallel Computing, 17,
pp 619-632. September 1991.
-
M. Munetomo, Y. Takai, Y. Sato. "An Efficient Migration
Scheme for Subpopulation-Based Asynchronously Parallel GAs". HIER-IS-9301,
Hokkaido University. July 1993.
-
T. Muntean, E. G. Talbi. "A Parallel Genetic Algorithm
for Process-Processors Mapping". Proceedings of the Second Symposium
II. High Performance Computing, M. Durán, E. Dabaghi (eds.),
pp 71-82. Montpellier, France: F. Amsterdam, Amsterdam. 1991.
-
NASA - Johnson Space Center. "Splicer - A Genetic Tool
for Search and Optimization". Genetic Algorithm Digest, Vol 5, Issue
17. 1991.
-
C. C. Pettey, M. R. Leuze, J. Grefenstette. "A Parallel
Genetic Algorithm". Proceedings of the 2nd ICGA, J. Grefenstette
(ed.), Lawrence Erlbraum Associates, pp 155-161. 1987.
-
J. C. Potts, T. D. Giddens, S. B. Yadav. "The Development
and Evaluation of an Improved Genetic Algorithm Based on Migration and
Artificial Selection". IEEE Transactions on Systems, Man, and Cybernetics,
24 (1), pp 73-86. January 1994.
-
N. J. Radcliffe, P. D. Surry. "The Reproductive Plan
Language RPL2: Motivation, Architecture and Applications". Genetic Algorithms
in Optimisation, Simulation and Modelling, J. Stender, E. Hillebrand,
J. Kingdon (eds.), IOS Press. 1994
-
I. Rechenberg. Evolutionstrategie: Optimierung Technisher
Systeme nach Prinzipien der Biologischen Evolution. Fromman-Holzboog
Verlag, Sttutg. 1973.
-
J. L. Ribeiro Filho, C. Alippi, P. Treleaven. "Genetic
Algorithm Programming Environments". Parallel Genetic Algorithms: Theory
& Applications, J. Stender (ed.), IOS Press. 1993.
-
G. Robbins. "EnGENEer - The Evolution of Solutions".
Proceedings of the 5th Annual Seminar on Neural Networks and Genetic
Algorithms. 1992.
-
N. N. Schraudolp, J. J. Grefenstette. "A Userís Guide
to GAUCSD 1.2". T. R. Computer Science & Engineering Department,
University of California, San Diego. 1991.
-
H. P. Schwefel. Numerical Optimization of Computer
Models. Wiley, Chichester. 1981.
-
W. M. Spears, K. A. De Jong. "An Analysis of Multi-Point
Crossover". Foundations of Genetic Algorithms, G. J. E. Rawlins
(ed.), Morgan Kaufmann, pp 301-315. 1991.
-
W. M. Spears. "Crossover or Mutation?". Proceedings
of the Foundations of Genetic Algorithms Workshop, D. Whitley (ed.),
Morgan Kaufmann, pp 221-237. 1992.
-
P. Spiessens, B. Manderick. "A Massively Parallel Genetic
Algorithm". Proceedings of the 4th International Conference on Genetic
Algorithms, R. K. Belew, L. B. Booker (eds.), Morgan Kaufmann, pp 279-286.
1991.
-
J. Stender (ed.). Parallel Genetic Algorithms: Theory
and Applications. IOS Press. 1993.
-
G. Syswerda. "A Study of Reproduction in Generational
and Steady-State Genetic Algorithms"; Foundations of GAs, G. J.
E. Rawlins (ed.), Morgan Kaufmann, pp 94-101. 1991.
-
R. Tanese. "Distributed Genetic Algorithms". Proceedings
of the 3rd International Conference on Genetic Algorithms, J. D. Schaffer
(ed.), Morgan Kaufmann, pp 434-439. 1989.
-
H. M. Voigt, J. Born, J. Treptow. "The Evolution Machine
Manual - V 2.1". T. R. in the Institute for Informatics and Computing
Techniques, Berlin. 1991.
-
H. M. Voigt, I. Santibáñez-Koref, J. Born.
"Hierarchically Structured Distributed Genetic Algorithms". Proceedings
of the International Conference Parallel Problem Solving from Nature, 2,
R. Männer, B. Manderick (eds.), North-Holland, Amsterdan, pp 155-164.
1992.
-
M.Wall. "Overview of Matthewís Genetic Algorithm Library".
http://lancet.mit.edu/ga.
1995.
-
D. Whitley. "The GENITOR Algorithm and Selection Pressure:
Why Rank-Based Allocation of Reproductive Trials is Best". Proceedings
of the 3rd. International Conference on Genetic Algorithms, J. D. Schaffer
(ed.), Morgan Kaufmann, pp 116-121. 1989.
-
D. Whitley, T. Starkweather. "GENITOR II: a Distributed
Genetic Algorithm". J. Expt. theor. Artif. Intelligence 2, pp 189-214.
1990.
This page was last updated on 6-May-98









