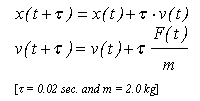Contents of this chapter
- VI.1 Background
- VI.2 GP for the Generation of Fuzzy Rules
VI.1 Background
(Sánchez, 1996)
In areas such as artificial intelligence, machine learning, or symbolic processing, we find
many problems whose resolution can be considered as the search of a computer program,
inside a space of possible programs that produce some desired outputs from the inputs.
This search should be carried out in such a way that the searched program be the more adequate
to the problem that we are considering.
The genetic programming (GP) paradigm provides us the appropriate framework to develop this type of search in
an efficient and versatile way, since it adapts to any problem type, i.e., it is very
robust.
The paradigm of genetic programming is based on the principle of survival of fittest
(C. Darwin). Starting from an randomly-generated initial population, it evolves populations
following this principle. The new individuals are a product of genetic operations on
the current population's better individuals. In connection with the genetic algorithms (GAs), GP
shares with these the philosophy and the characteristics of being heuristic and stochastic.
VI.1.1 The GP Paradigm in Machine Learning
Inside the area of the machine learning, we find several paradigms focused toward the
resolution of problems. In each paradigm the used structures
are different:
 Connectionist Model: the solution to
the problem is given as a group of real-valued weights that indicate if the value of the signal
that goes by a certain connection of a neural network is amplified or diminished.
Connectionist Model: the solution to
the problem is given as a group of real-valued weights that indicate if the value of the signal
that goes by a certain connection of a neural network is amplified or diminished.
Application field: NEURAL NETWORKS
 Evolutionary Model: the solutions
are fixed-length strings (in the classic model). Each chromosome represents a possible
solution to the problem. A conventional genetic algorithm is applied to obtain
the best solution (or a good enough solution) among all possible solutions.
Evolutionary Model: the solutions
are fixed-length strings (in the classic model). Each chromosome represents a possible
solution to the problem. A conventional genetic algorithm is applied to obtain
the best solution (or a good enough solution) among all possible solutions.
Application field: GENETIC ALGORITHMS
 Inductive Model: according to this paradigm the
solutions to a certain problem are given by decision trees. Each one of these trees
classifies each instance of the problem in classes, for which a possible solution exists.
Inductive Model: according to this paradigm the
solutions to a certain problem are given by decision trees. Each one of these trees
classifies each instance of the problem in classes, for which a possible solution exists.
Application field: CLASSIFFIER SYSTEMS
Each one of the mentioned models can be more or less effective solving a certain problem
type. The approach that is used to determine the efficiency of a method is, in the first
place, the flexibility to adapt to several types of problems, and in second its easiness to
represent the solutions to this problem in a natural and comprehensible way for the user.
Computer programs offer flexibility:
This idea of flexibility includes the concepts of flexibility in the size, the form and the
structural complexity of the solution. That is to say, the user should avoid stating
any type of explanation or previous imposition on the size or form of the solution. The true
power of GP resides in its capacity of adaptation to the problem, for what the considerations
on the size, the complexity or the form of the solution should emerge during the own resolution
process.
The importance of the representation of the solutions resides in that the genetic algorithms
manipulate the structure of this representation directly and not the own solution.
String-representations do not directly provide the hierarchical structure
of programs. Also, the adaptation of the form, size and complexity of individuals becomes very
difficult. Therefore, GP has spread toward more complex representations that contribute the
needy flexibility. Smith introduces the strings of variable length and IF-THEN-ELSE
components (Smith, 1980).
Genetic algorithms are used in a wide range of applications thanks to the adaptation of
their evolutionary structures. For example as classification systems, as the system designed by
Wilson for the classification of boolean functions
(Wilson, 1987). Goldberg introduced the Messy genetic algorithms that handle populations of
individuals represented by strings of characters of variable length
(Goldberg, 1989b).
GP uses programs like individuals, but the division of opinions appears with its implemnetation.
Cramer uses strings of characters of constant length to generate programs with a certain
structure (Cramer, 1985). Fujiki and Dickinson have
developed a system that is based on the generation of programs that use simple conditional
sentences of LISP (COND) (Fujiki, Dickinson, 1987).
As we have already seen, the resolution of many problems can be modelled as an evolutionary
process in which the fittest individual survive. The simulation of this evolutionary process
begins with the aleatory generation of an initial
population, composed by computer programs that represent the individuals. These programs are
generated starting from the group of functions and terminal elements that adapt better to the
problem to solve. In most cases, the election of the group of terminal and non terminals
(functions) is critical to make the algorithm works properly.
For example, if we want to generate complex mathematical functions it is interesting to
introduce in the group of non terminals such functions as sines, cosines, and so on. For
graphic applications, it is usually quite normal
to introduce primitive of the type Line, Circle, Torus that graphically represent figures in diverse ways.
The appropriateness of each program is measured in terms of how of
well it performs in the environment of the particular problem. This measure is denominated fitness.
A program is generally evaluated in different representative cases, and the final measure of
its fitness will be an average of all the measures (one for each case). Usually, the result of the genetic algorithm is the best individual
generated in generation n, being n the maximum number of generations.
GP performs, in a genetic way, computer programs executing the three following steps:
|
1) Randomly generate the initial population, using the group of
terminals and functions for the considered problem.
2) Iteralively carry out the following steps until the termination criterion is satisfied:
a) Execute every individual's program and assign it a fitness value, according to
its ability to solve the problem.
b) Create a new population applying genetic operators on the selected individuals:
i) Reproduction.
ii) Crossover.
3)Take the best solution of the final population.
|
Figure 1. Steps of a GP.
VI.2 GP for the Generation of Fuzzy Rules
(Alba, Cotta, Troya, 1996)
In this section, we describe an application of GP in which individuals (trees) are not computer programs in
a traditional sense. Every tree will represent a set of fuzzy rules intended to solve a control
problem (the cart centering problem -Figure 2-, described and analytically solved in
(Koza, 1992)).
The underlying target programming language is neither C, PASCAL nor LISP. We use a fuzzy
interpreter in order to compile and run the resulting fuzzy rules on our specific problem.
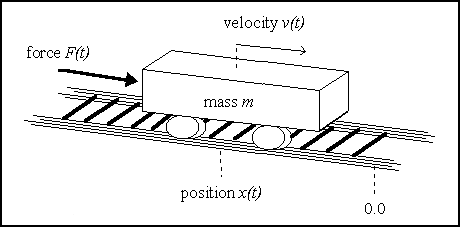
Figure 2. The Cart Centering Problem.
VI.2.1 Fuzzy Logic Controllers
A Fuzzy Logic Controller (FLC) is a rule-based system that tries to incorporate the
flexibility of human-decision making by means of the use of fuzzy set theory (Lee, 1990).
The rules of an FLC incorporate fuzzy linguistic terms (e.g. temperature is warm) described by
membership functions. These functions are intended to represent human expert's conception of the
linguistic terms, thus giving an approximation of the confidence with which a precise numeric
value is described by a linguistic label.
Rules take the form IF [conditions] THEN [actions], where conditions and actions are
linguistic labels applied to input and output variables respectively (e.g. IF temperature
IS hot THEN refrigeration IS high). A set of such fuzzy rules constitutes the fuzzy rule-base
of the FLC. The system uses this rule-base to produce precise output values according to
actual input values. This control process is divided into three stages:
- fuzzification: calculate fuzzy input, i.e. evaluate input variables with respect to the
corresponding linguistic terms in the condition side.
- fuzzy inference: calculate fuzzy output, i.e. evaluate activation strength of every rule
and combine their action sides.
- defuzzification: calculate actual output, i.e. convert fuzzy output into a precise numerical
value.

Figure 3. Phases of fuzzy interpreter.
The fuzzy interpreter used in this work performs fuzzification via triangular membership
functions, uses the min intersection operator, the maxmin method for fuzzy inference and the
centroid procedure for defuzzification (for comparation purposes with (Thrift, 1991)).
VI.2.2 The Cart Centering Problem
In this section a description of the cart centering problem will be made. Next, it will be
shown how the principles of fuzzy control can be applied to this problem, outlining an ad-hoc
solution.
A cart with mass m can move along an infinite one-dimensional frictionless track. The
problem consists in centering the cart, in minimal time, by applying an external time-variant
force (of maximal magnitude F) so as to accelerate the cart in either the positive or
the negative direction of the track.
This problem can be further formulated as calculating a force F(t) = F[x(t), v(t)] in
order to place the cart in position x(tf)=0 with velocity v(tf)=0 in minimal
tf.
The exact time-optimal solution consists in applying a force F(t)=F when
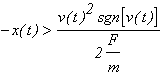 and -F otherwise.
and -F otherwise.
This system can be simulated using Euler's method considering time steps ( ):
):
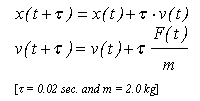
As an optimal control problem, the cart centering problem is well-suited for fuzzy control.
In order to develop an FLC for this system we take several steps:
- Determation of the condition (input) vbles.-> position x(t) and velocity v(t).
- Definition of the membership functions representing the fuzzy sets over these inputs (5
partitions: NegLarge/NegSmall/Zero/PosSmall/PosLarge).
- Identification of action (output) variables -> the force F(t) applied to the cart.
We use the same fuzzy sets above to describe this output variable.
- Production of the rule-base. This set of rules might have been designed by a human expert.
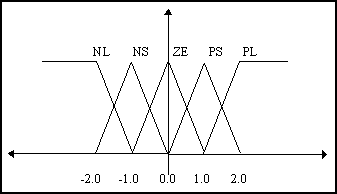
Figure 4. Fuzzy sets for position, velocity and force.
VI.2.3 A Hand-Made Fuzzy Solution
We can define a human-expert conception of a solution as follows:
The applied force must almost always be directed towards the origin (since we want to
place the cart in the 0 position) and, just when we are close to that point, we must reverse
that force to stop the cart
The associated FLC rule-base can be expressed as:
- IF pos IS PL THEN for IS NL
- IF pos IS PS THEN for IS NL
- IF pos IS ZE AND vel IS PL THEN for IS NL
- IF pos IS ZE AND vel IS PS THEN for IS NL
- IF pos IS ZE AND vel IS NS THEN for IS PL
- IF pos IS ZE AND vel IS NL THEN for IS PL
- IF pos IS NS THEN for IS PL
- IF pos IS NL THEN for IS PL
The FLC defined by the membership functions and the rule-base described above is not the
optimal one. It can be improved by means of a learning technique that modifies the rule set or
the interpretation of the linguistic terms. Genetic algorithms have been used for that purpose
in both ways (Thrift, 1991),
(Karr, 1991),
(Lee, Takagi, 1993),
(Feldman, 1993). We propose the use of GP to
produce rule bases that can be used as a starting point for further refinements by a human
expert.
VI.2.4 Advantages of using Genetic Programming
 No analytical knowledge is needed and we can still
get accurate results.
No analytical knowledge is needed and we can still
get accurate results. If we encode fuzzy sets in the genotype we can
generate new -more suited- fuzzy sets to describe precise and individual membership functions.
We can do it by means of the intersection and/or union of the existing fuzzy sets.
If we encode fuzzy sets in the genotype we can
generate new -more suited- fuzzy sets to describe precise and individual membership functions.
We can do it by means of the intersection and/or union of the existing fuzzy sets. Every component of the resulting GP rule-base is
relevant in some way for the solution of the problem. Thus we do not encode null operations that
will expend computational resources at runtime.
Every component of the resulting GP rule-base is
relevant in some way for the solution of the problem. Thus we do not encode null operations that
will expend computational resources at runtime. This approach does scale with the problem size. Some
other approaches to the cart centering problem use a GA that encodes NxN matrices of parameters.
These solutions work bad as the problem grows in size (i.e. as N increases).
This approach does scale with the problem size. Some
other approaches to the cart centering problem use a GA that encodes NxN matrices of parameters.
These solutions work bad as the problem grows in size (i.e. as N increases). With GP we do not impose restrictions on how the
structure of solutions should be. Also we do not bound the complexity or the number of rules of
the computed solution.
With GP we do not impose restrictions on how the
structure of solutions should be. Also we do not bound the complexity or the number of rules of
the computed solution.
VI.2.5 Genetic Programming of Fuzzy Logic Controllers
1. Encoding a Rule-Base
As stated above, the rule-base of the FLC is a list of IF-THEN rules. Each of them can be
easily represented as a binary tree: the root being an IF node and left and right branches
representing the condition and the action sides respectively. Likewise, both conditions and
actions can be expressed as trees. On the one hand, a variable paired with a fuzzy set can be
represented as a tree with an IS root-node, the variable name in the left branch and the fuzzy
set in the right branch. On the other hand, a conjunction of such terms can be expressed as a
tree with an AND root-node and two branches representing nested conjunctions or pairs (variable,
fuzzy set). Figure 5 shows an example.
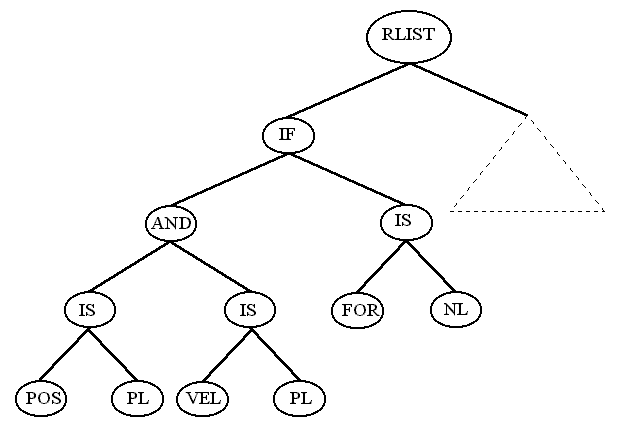
Figure 5. A syntactic tree and the rule it represents.
| BNF GRAMMAR OF TREES |
<TREE>
<RLIST>
<IF>
<COND>
<L_IS>
<L_AND>
<ACT>
<R_IS>
<R_AND>
<SET>
<VBLEIN>
<VBLEOUT>
|
::= EL | <IF> | <RLIST>
::= <TREE> <TREE> RLIST
::= <COND> <ACT> IF
::= <L_IS> | <L_AND>
::= <VBLEIN> <SET> LEFT_IS
::= <COND> <COND> LEFT_AND
::= <R_IS> | <R_AND>
::= <VBLEOUT> <SET> RIGHT_IS
::= <ACT> <ACT> RIGHT_AND
::= NL | NS | ZE | PS | PL
::= VEL | POS
::= FOR
|
Likewise, both conditions and actions can be expressed as trees with an IS root-node,
the (in/out) variable name in the left branch and the fuzzy set in the right branch. A
conjunction of such terms can be expressed as a tree with an AND root-node and two nested
conjunctions branches.
2. Add types to the Trees
The flexibility of our tree representation makes crossover a very powerful tool since it
allows interchange at several levels: rules, terms or even variables and fuzzy sets. Since
traditional crossover may produce nonsense rules we can:
 Define closed functions, so the ill-defined
rules could be interpreted in some given way, e.g. computing fixed values for unexpected
symbols.
Define closed functions, so the ill-defined
rules could be interpreted in some given way, e.g. computing fixed values for unexpected
symbols. Repair the tree, deleting (adding) incorrect
(new) subtrees.
Repair the tree, deleting (adding) incorrect
(new) subtrees. Perform a restricted crossover, i.e.
resulting trees will be correct.
Perform a restricted crossover, i.e.
resulting trees will be correct.
Since the first option will produce a high number of useless trees (dummy rules) and the
second one is computationally expensive and will produce offsprings very
different with respect to the parents, we have chosen the third option.
Crossover selects one random subtree from every parent. The selection of the root nodes of
the two subtrees is forced to have the same type.
| TYPE |
SYMBOLS |
| Type I |
{ IF, RLIST, EL } |
| Type II |
{ AND, IS } |
| Type III |
{ ... variable names ... } |
| Type IV |
{ ... fuzzy sets ... } |
3. Refine types to keep consistency
 The presented types will lead to the creation of
syntactically correct but semantically incorrect trees => a rule could be spawned in which output
variables appear in the condition side and/or input variables appear in the action side (e.g.
IF for IS NL THEN pos IS ZE).
The presented types will lead to the creation of
syntactically correct but semantically incorrect trees => a rule could be spawned in which output
variables appear in the condition side and/or input variables appear in the action side (e.g.
IF for IS NL THEN pos IS ZE). If this kind of situations were allowed, the GP
system would waste valuable resources in evaluating and storing such useless rules. To avoid
this problem, we define two subtypes for both types II and III.
If this kind of situations were allowed, the GP
system would waste valuable resources in evaluating and storing such useless rules. To avoid
this problem, we define two subtypes for both types II and III. Every subtype can be seen as the variety of the
corresponding type that appears in either the condition or the action side.
Every subtype can be seen as the variety of the
corresponding type that appears in either the condition or the action side.
| TYPE |
MEANING |
SUBTYPES |
MEANING |
| LIST |
List of rules |
- |
- |
| COND_ACT |
Condition or Action |
CONDITION
ACTION |
To separate branches of an IF structure |
| VBLE |
Variable |
VBLE_IN
VBLE_OUT |
Input variable
Output variable |
| SET |
Fuzzy Set |
- |
- |
4. Conclusions
The GP design of fuzzy logic controllers is a more flexible and natural way that traditional
GAs since no a priori constraints are posed on the shape of the solution (in fact this shape
also evolves): the complexity of the solutions are not bounded by the algorithm.
By including fuzzy sets in the trees we can also evolve them through their union and
intersection, thus refining initially (hand-crafted) user proposed fuzzy set.
A typed system that defines the composition of the solution trees allows to keep strings
feasibility at runtime at a low cost and prevents the GA of useless wanderings along the search
space => more complex problems can be tackled.
The GP solution clearly outperforms intuitive solutions and is competitive with other
genetic-based solutions regarding the time to dock the cart and in keeping a low level of
complexity and the number of fuzzy rules.
This page was last updated on 21-Nov-97
 Connectionist Model: the solution to
the problem is given as a group of real-valued weights that indicate if the value of the signal
that goes by a certain connection of a neural network is amplified or diminished.
Connectionist Model: the solution to
the problem is given as a group of real-valued weights that indicate if the value of the signal
that goes by a certain connection of a neural network is amplified or diminished. Evolutionary Model: the solutions
are fixed-length strings (in the classic model). Each chromosome represents a possible
solution to the problem. A conventional genetic algorithm is applied to obtain
the best solution (or a good enough solution) among all possible solutions.
Evolutionary Model: the solutions
are fixed-length strings (in the classic model). Each chromosome represents a possible
solution to the problem. A conventional genetic algorithm is applied to obtain
the best solution (or a good enough solution) among all possible solutions. Inductive Model: according to this paradigm the
solutions to a certain problem are given by decision trees. Each one of these trees
classifies each instance of the problem in classes, for which a possible solution exists.
Inductive Model: according to this paradigm the
solutions to a certain problem are given by decision trees. Each one of these trees
classifies each instance of the problem in classes, for which a possible solution exists.

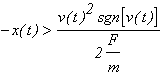 and -F otherwise.
and -F otherwise. ):
):