VIII. |
HYBRIDIZATION OF EC ALGORITHMS |
Contents of this chapter
- VIII.1 GA + Branch and Bound
VIII.1 GA + Branch and Bound
(Cotta, Aldana, Nebro, Troya, 1995)
GAs and B&B techniques are in some way antithetical methods for combinatorial-optimization-problem
solving, at least with regard to the observable characteristics during the solving of such a problem.
A straightforward comparison of both methods yields the following considerations:
 B&B techniques allow a fast problem solving since the
heuristics they incorporate ease a direct advance to solutions, rejecting those paths that do not drive
the algorithm to an optimum (achieving it is guaranteed). In contrast, a GA is a quite slow procedure
since it only takes in account the relative fitness of some approximate solutions. In fact, and unlike
B&B techniques, those solutions that might be considered bad are not rejected because they may carry
any important feature in order to solve the problem. It is important to realize that obtaining the
optimum is not guaranteed by means of GAs.
B&B techniques allow a fast problem solving since the
heuristics they incorporate ease a direct advance to solutions, rejecting those paths that do not drive
the algorithm to an optimum (achieving it is guaranteed). In contrast, a GA is a quite slow procedure
since it only takes in account the relative fitness of some approximate solutions. In fact, and unlike
B&B techniques, those solutions that might be considered bad are not rejected because they may carry
any important feature in order to solve the problem. It is important to realize that obtaining the
optimum is not guaranteed by means of GAs. GAs are more suitable for large instances of a problem. The
key factor of their functioning is not the store space (whose utilization remains constant during the
execution) but execution time which may be very large. As a matter of fact, indefinitely executing a GA
will, theoretically, yield the optimal solution of the problem being solved. On the other hand, a B&B
algorithm will fail solving a very large problem due to the resulting combinatorial explosion.
GAs are more suitable for large instances of a problem. The
key factor of their functioning is not the store space (whose utilization remains constant during the
execution) but execution time which may be very large. As a matter of fact, indefinitely executing a GA
will, theoretically, yield the optimal solution of the problem being solved. On the other hand, a B&B
algorithm will fail solving a very large problem due to the resulting combinatorial explosion.
The features above make difficult to combine both techniques as shown next.
VIII.1.1 Direct collaboration. Issues
A first possibility for GAs and B&B techniques to work together is executing both procedures
independently and in parallel, that is, at the same level. Both processes will enclose the solution but
coming from different directions: the GA will provide an upper bound of the optimal solution whilst the
B&B algorithm produces a lower bound of it. Those bounds will become closer and closer along the execution.
There are two ways of obtaining a benefit of this parallel execution:
 Use the upper bounds provided by the GA to purge the problem
queue of the B&B algorithm, deleting those subproblems whose lower bound is bigger than the one obtained
from the GA.
Use the upper bounds provided by the GA to purge the problem
queue of the B&B algorithm, deleting those subproblems whose lower bound is bigger than the one obtained
from the GA. Inject into the GA information about those subtours the B&B
algorithm considers more promising. They would be the building blocks of the TSP representation.
Inject into the GA information about those subtours the B&B
algorithm considers more promising. They would be the building blocks of the TSP representation.
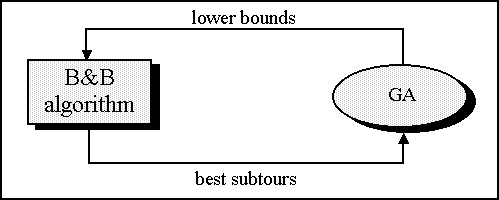
Figure 1. Direct collaboration scenario.
These options are, however, difficult to carry out for many reasons:
 Execution times are quite disparate, so establishing an effective
information exchange is very difficult. For example, consider the negative effect resulting from injecting
some high-valued building blocks (whose presence in the optimal solution is besides not guaranteed) in early
stages of the GA, in which the population is a fairly homogeneous set of rather poor solutions. This might
seriously affect diversity, thus polarizing further evolution in a wrong way.
Execution times are quite disparate, so establishing an effective
information exchange is very difficult. For example, consider the negative effect resulting from injecting
some high-valued building blocks (whose presence in the optimal solution is besides not guaranteed) in early
stages of the GA, in which the population is a fairly homogeneous set of rather poor solutions. This might
seriously affect diversity, thus polarizing further evolution in a wrong way. There is a big gap between the accuracies of both methods.
Specifically for the TSP, B&B algorithms start from an initial approximation that is usually within a 2% of
the optimum, and work in that range seldom producing a subproblem with a lower bound much greater than the
optimum. On the other hand, GAs do not usually achieve a high accuracy and when they do it occurs in late
stages of evolution, so it is too late for a B&B algorithm to get a benefit by purging the problem queue.
There is a big gap between the accuracies of both methods.
Specifically for the TSP, B&B algorithms start from an initial approximation that is usually within a 2% of
the optimum, and work in that range seldom producing a subproblem with a lower bound much greater than the
optimum. On the other hand, GAs do not usually achieve a high accuracy and when they do it occurs in late
stages of evolution, so it is too late for a B&B algorithm to get a benefit by purging the problem queue.
Clearly, it is necessary to find an alternative approach in order to establish a productive collaboration
between both techniques. At first and according to the functioning features mentioned, there exist two ways
of harmonizing their performances, each one focusing in trying to make use of one of the collaboration
options above. On the one hand, it is possible to reduce the combinatorial explosion which limits the
effectiveness of a B&B algorithm by imposing some restrictions to the problem. On the other hand, parallel
execution of many GAs may heighten their power.
The first option is represented by a strategy which has produced good results in a wide range of problems:
build and Hybrid Genetic Algorithm (HGA). For the second one, it is more interesting a mixed approach
(including restrictions in the B&B side too) than a pure one.
VIII.1.2 Branch and Bound working for a Genetic Algorithm
In the model described next, the GA plays the role of a master and the B&B algorithm is incorporated as a
tool of it. From the point of view of the GA, this is perhaps the most elegant option and the one that implies
a bigger cohesion.
VIII.1.2.1 Hybridizing a Genetic Algorithm
As mentioned, the key feature of a GA is its robustness: binary representation and simple binary crossover and
mutation operators provide problem-domain independence. However, such an algorithm will never be the best to
solve a certain problem because, as in nature, every niche (optimization problem) is dominated by species
(algorithms) specifically adapted to it. In fact, almost every specialized algorithm will outperform a GA.
It is possible, anyway, to improve a GA performance applying some techniques and knowledge used by other
algorithms, although this implies a loss of robustness. There are three main principles in order to incorporate
those items:
 Use the encoding of the specialized algorithm.
Use the encoding of the specialized algorithm. Incorporate, where possible, those positive features of the specialized
algorithm.
Incorporate, where possible, those positive features of the specialized
algorithm. Adapt the genetic operators, using domain-specific heuristics and procedures.
Adapt the genetic operators, using domain-specific heuristics and procedures.
Basically, the principles above show that a good use of all the theoretical basis of the specialized algorithm
must be done. For example, the representation function of it will usually be based on experience in solving that
problem, so its use will exploit that domain-knowledge. On the other hand, the specialized algorithm will normally
use an efficient procedure to interpret that encoding and it can be also included in the HGA.
VIII.1.2.2 A Hybrid Genetic Algorithm to solve the TSP
To hybridize a GA incorporating B&B techniques and knowledge requires applying the principles mentioned above. A promising
way of doing that is to build a hybrid operator with the philosophy of B&B. The idea underlying this option is shown next.
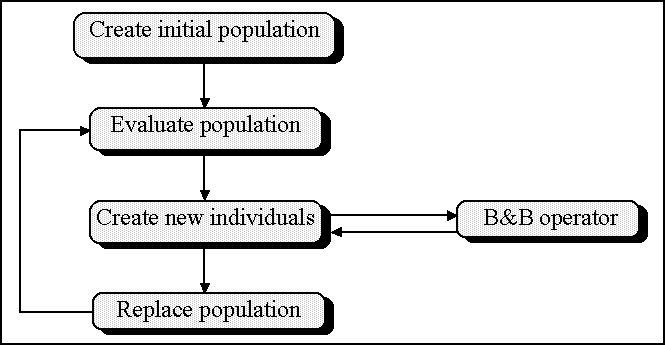
Figure 2. Outline of the Hybrid Genetic Algorithm (HGA).
As mentioned, the information related to the goodness of a certain tour is contained in the edges between nodes (in fact,
they carry the weights of a connection). This information must be transmitted generation to generation using the genetic operators.
Specifically, the information carried by some ancestors should be recombined to create some offsprings using a crossover operator.
However, the classical existing operators usually introduce a great amount of new information since the produce offsprings including
edges not appearing in any ancestor. That is why some advanced operators, such as Edge-Recombination, are created. This one
guarantees that an offspring will inherit a 95% of its genetic information from its ancestors. The operator described next
assures that an unique offspring will be created using only edges from the ancestors (i.e. without any implicit mutation).
The functioning of this operator is as follows: the B&B algorithm starts from a list of all edges in the graph with information
related with associated weights. This operator is a restricted version of the B&B algorithm in which only the edges that appear in
the ancestors are taken into account . The offspring obtained will not only 100% composed by its ancestors’ edges but it will also
be the best solution that can be build using those edges (i.e. the operator has a high heuristic charge).
The net effect of this operator is to link low-cost subtours existing in the ancestors, or their construction. In fact, considering
these elements as the building blocks of the problem the B&B algorithm would build them and glue together (injecting them into the GA
as mentioned in 6.1).
VIII.1.2.3 Aspects of the hybrid operator use
It is clear that the restricted TSP solution carried out by the described operator is faster and does not have the memory limitations
of the base case since it turns from solving a problem with (n^2)/2 edges to another with 4n edges in the worst case. However, this operator
is going to be used a high number of times and its computational complexity is much higher than other operators such as edge-recombination,
so the execution time of a GA that makes an intensive use of this operator might reach untenable values.
The first preventive measure in order to decrease the computational effort of the algorithm is a combined use of many crossover operators.
Since the hybrid-operator complexity is determined by the number of edges taken into account, its use could be restricted to those occasions
in which the ancestors share a good amount of edges (in the best case -the trivial one- only n edges are considered), using a standard operator
in any other situation. A feasible model involves calculating the number of different edges of both ancestors, normalizing it (considering that
the minimum is n and the maximum is 4n), and performing a random test based on this number in order to select which operator to use, the hybrid
one or the standard one.
The described model has not only the advantage of reducing execution time but it also mitigate another drawback of the operator, the greediness
of its heuristic functioning. This behaviour may even cause that no recombination takes place (when the best way to combine the edges is precisely
one of the ancestors). Standard edge-recombination operator can produce offsprings whose fitness value is lower than the ancestors’ and introduce
a little amount of mutation too. In this way, using the model above resembles a thermodynamic system: in early stages temperature (disparity
between individuals) is high and the standard operator is often used, thus grouping building blocks. As the system freezes the heuristic operator
becomes more used. In those late stages the probability of an important block not being carried due to the greediness of the operator is lower.
Another less desirable side effect of this operator is the tendency to a fast convergence that induces in the GA. Combining two rather poor individuals
may frequently result in offsprings with a much higher fitness value than the ancestors. The apparition of these superindividuals (Davis, 1991b)
may lead to a big loss of diversity and the sooner it occurs the more dangerous it is. This effect can be relieved introducing a higher mutation rate,
with the risks that come with it.
VIII.1.2.4 Improving the model. Parallelism
In spite of the use of the described model, execution times (although decreased) are still high so another strategy must be used to optimize the
process. One of the most suitable options is parallelizing it. There exists some alternatives in order to carry out that parallelization. The following
ones can be mentioned:
 Parallelizing the hybrid operator: this option would only reduce the execution time of the GA, remaining
unaltered its behaviour.
Parallelizing the hybrid operator: this option would only reduce the execution time of the GA, remaining
unaltered its behaviour. Overlapping the hybrid operator with the rest of the GA: this option consists of the parallel launching of
many hybrid crossover operations. The GA continues its functioning without waiting for these operations to be concluded. As they finish the generated
offsprings are inserted into the population. This option do introduce qualitative behaviour differences in relation to the sequential version. The main
one is the absolute disappearance of the generation concept since a great gapping occurs (individuals resulting from crossover operations launched many
iterations before are inserted into the population).
Overlapping the hybrid operator with the rest of the GA: this option consists of the parallel launching of
many hybrid crossover operations. The GA continues its functioning without waiting for these operations to be concluded. As they finish the generated
offsprings are inserted into the population. This option do introduce qualitative behaviour differences in relation to the sequential version. The main
one is the absolute disappearance of the generation concept since a great gapping occurs (individuals resulting from crossover operations launched many
iterations before are inserted into the population).
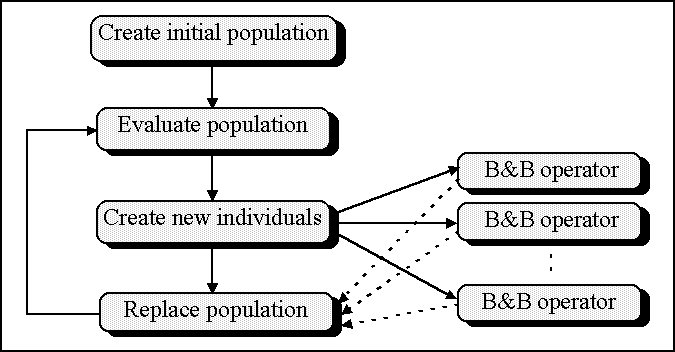
Figure 3. Outline of the Asynchronous Hybrid Genetic Algorithm (AHGA).
It is possible that this overlapping provides a positive side effect: problems related to superindividuals where mentioned in 4.3.3. However, inserting
them in the population many evolutionary cycles later may allow average fitness to increase enough not to suffer (or to suffer less) because of the
presence of those individuals.
VIII.1.3 Branch and Bound and parallel evolution
The other way to close up characteristics of B&B techniques and GAs is to heighten the power of the later ones in order to adequate them to a B&B speed.
This heightening can be achieved by means of parallelly executing many GAs. This is a very general model since GAs can execute independently or establish
some kind of collaboration between them, periodically interchanging a part of their populations (Suárez, 1994).
VIII.1.3.1 Describing the model
In the simplest scenario, a B&B algorithm executes in parallel with a certain number of GAs. It is possible that many GAs provide good bounds in less time,
although they will generally produce solution of similar magnitude and different structure, so the problem queue will seldom be purged (though in the worst
case it equals the direct collaboration model). Consequently, it is necessary to develop a more complex model.
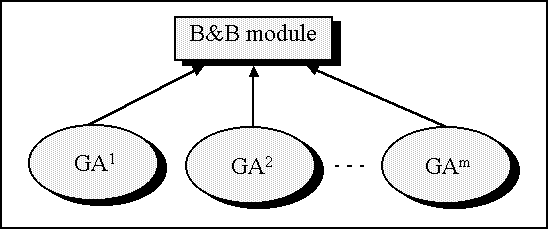
Figure 4. Outline of the parallel evolution model.
Notice one of the main problems of the B&B algorithm when applied to the TSP: a high number of edges must be considered. The complexity of the algorithm can
be decreased by reducing this number of edges. Two extreme situations are the base case (in which every edge is taken into account) and the described hybrid
operator (which only considers edges from two individuals). There exist intermediate positions between these extremes that consider a higher or lower number
of edges. In order to delete those "bad" edges information from the GAs can be used.
The model outlined above can be described as follows. There is a generalized hybrid operator that recombines n individuals. Such operator is placed in a
master process that controls m GAs, where n = k·m. Periodically, every GA send to the operator k individuals (e.g. the best k). The probable diversity in the
structure of individuals provided by independent GAs will contribute to make that almost every edge suitable to be part of the optimal solution be included
in any individual, and many non-suitable edges will not be taken into account.
VIII.1.3.2 Variations and improvements
There exist many variations that take as reference the strategy above. two fairly significant ones are:
 Perform an information exchange between GAs as stated in any of the migratory models described in (Suárez, 1994). Although
this action may improve a GA, perhaps it would make diversity of solutions generated by independent GAs decrease, and this would not be good for the B&B stage.
Perform an information exchange between GAs as stated in any of the migratory models described in (Suárez, 1994). Although
this action may improve a GA, perhaps it would make diversity of solutions generated by independent GAs decrease, and this would not be good for the B&B stage. Take n = k·m+1, that is, send to the hybrid operator not only the individuals provided by the GAs but also the best obtained so far. This is the B&B counterpart
of GA elitism, since it guarantees that the best calculates solution is, at least, conserved at the expense of considering more edges.
Take n = k·m+1, that is, send to the hybrid operator not only the individuals provided by the GAs but also the best obtained so far. This is the B&B counterpart
of GA elitism, since it guarantees that the best calculates solution is, at least, conserved at the expense of considering more edges. Inject into the GAs the individual created by the hybrid operator. This is a dangerous action since it may cause convergence problems. In order to alleviate
this drawback, some options are suggested:
Inject into the GAs the individual created by the hybrid operator. This is a dangerous action since it may cause convergence problems. In order to alleviate
this drawback, some options are suggested:
- Do not send back the generated individual to the GAs until a certain number of generations is reached.
Send back an individual to a GA only if the difference between its fitness and that of the best individual in this GA does not exceed a certain threshold.
Send back to a GA the result of recombining the generated individual and the individual which that GA sent using a standard operator.
No experiences have been done in order to assure the goodness of the strategies above.
This page was last updated on 21-Nov-97
 B&B techniques allow a fast problem solving since the
heuristics they incorporate ease a direct advance to solutions, rejecting those paths that do not drive
the algorithm to an optimum (achieving it is guaranteed). In contrast, a GA is a quite slow procedure
since it only takes in account the relative fitness of some approximate solutions. In fact, and unlike
B&B techniques, those solutions that might be considered bad are not rejected because they may carry
any important feature in order to solve the problem. It is important to realize that obtaining the
optimum is not guaranteed by means of GAs.
B&B techniques allow a fast problem solving since the
heuristics they incorporate ease a direct advance to solutions, rejecting those paths that do not drive
the algorithm to an optimum (achieving it is guaranteed). In contrast, a GA is a quite slow procedure
since it only takes in account the relative fitness of some approximate solutions. In fact, and unlike
B&B techniques, those solutions that might be considered bad are not rejected because they may carry
any important feature in order to solve the problem. It is important to realize that obtaining the
optimum is not guaranteed by means of GAs. GAs are more suitable for large instances of a problem. The
key factor of their functioning is not the store space (whose utilization remains constant during the
execution) but execution time which may be very large. As a matter of fact, indefinitely executing a GA
will, theoretically, yield the optimal solution of the problem being solved. On the other hand, a B&B
algorithm will fail solving a very large problem due to the resulting combinatorial explosion.
GAs are more suitable for large instances of a problem. The
key factor of their functioning is not the store space (whose utilization remains constant during the
execution) but execution time which may be very large. As a matter of fact, indefinitely executing a GA
will, theoretically, yield the optimal solution of the problem being solved. On the other hand, a B&B
algorithm will fail solving a very large problem due to the resulting combinatorial explosion.


