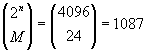
ECC Problem Description
There are many kinds of error correcting codes; we will work with binary linear block codes. As we often find in optimization problems we have two conflicting requirements to solve this problem. First we try to find minimum length codewords so that we ensure quickly transmission of messages encoded using these codewords. On the other hand, the Hamming distance between codewords must be maximized to guarantee good error correction.
A block error correcting code can be represented depending on three parameters, (n, M, d), where n is the number of bits in each word in a code, M is the number of words in the code; and d is the minimum Hamming distances between any pair of words in the code. The maximum number of single bit errors that a code word with distance d can correct is (d-1)/2.
An optimal code is one that maximizes d, given n and M. We solve the problem for a M=24 words code, with n=12 bits length codewords. If exhaustive search is used then the search space is 1087 which is the result of
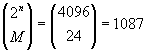
The optimization criteria is based on a measurement of how well the M words are placed in the corners of an n-dimensional space by considering the minimal energy configuration of M particles (where dij is the Hamming distance between words i and j:
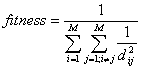 (Eq.1)
(Eq.1) We will find optimal correction codes with 24 words of 12 bits length. A possible optimal solution to the problem is shown below:
|
Words
|
Matrix of distances with other words
|
|
000011101010
000100111111 000111010100 001000110000 001001001101 001110000011 010000000110 010010011001 010101100001 011011110111 011101011010 011110101100 100001010011 100010100101 100100001000 101010011110 101101100110 101111111001 110001111100 110110110010 110111001111 111000101011 111011000000 111100010101 |
0 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6
6 6 6 6 12
6 0 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 12 6 6 6 0 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 12 6 6 6 6 6 0 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 12 6 6 6 6 6 6 6 0 6 6 6 6 6 6 6 6 6 6 6 6 6 6 12 6 6 6 6 6 6 6 6 6 0 6 6 6 6 6 6 6 6 6 6 6 6 12 6 6 6 6 6 6 6 6 6 6 6 0 6 6 6 6 6 6 6 6 6 6 12 6 6 6 6 6 6 6 6 6 6 6 6 6 0 6 6 6 6 6 6 6 6 12 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 0 6 6 6 6 6 6 12 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 0 6 6 6 6 12 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 0 6 6 12 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 0 12 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 12 0 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 12 6 6 0 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 12 6 6 6 6 0 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 12 6 6 6 6 6 6 0 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 12 6 6 6 6 6 6 6 6 0 6 6 6 6 6 6 6 6 6 6 6 6 6 12 6 6 6 6 6 6 6 6 6 6 0 6 6 6 6 6 6 6 6 6 6 6 12 6 6 6 6 6 6 6 6 6 6 6 6 0 6 6 6 6 6 6 6 6 6 12 6 6 6 6 6 6 6 6 6 6 6 6 6 6 0 6 6 6 6 6 6 6 12 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 0 6 6 6 6 6 12 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 0 6 6 6 12 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 0 6 12 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 0 |
Table 1. An optimal solution to ECC problems and its associated matrix of distances.
Since the fitness
function in a high grade determine the behavior of an evolutionary algorithm
when solving a problem, it is very important how this one is designed. In
these section we will address the definition of the fitness function and interpretation
of the string being manipulated in the GAs intended to guide the algorithm
towards the problems region where we find the solution.
In our representation, the words in the code being a tentative
solution to the problem are represented as a concatenated bit string which
is manage in the GA. To get the solution from an individual we just have to
slice the bit string into M pieces of n bits length.
We will investigate the relative performances of two evaluation
functions. The first one Evaluate1, is a fitness function that directly follows
the problem definition (equation 1), thus measuring how well the words in
the code are placed in the corners of a n-dimensional space. In equation
1 we can see that we maximize hamming distance between each pair of words
in the code. Exactly, the function Evaluate1 assign better fitness values
to that individuals whose hamming distances between words are greater, by
computing the inverse of the sum of inverses of all these distances to the
second.
After design and testing the first function and in an attempt
to get better results we introduce the second function, Evaluate2. This new
function arise as an improvement of the first one. Two main improvements are
made to the first function: (1) we can easily observe that we can save computing
twice hamming distances for dij and dji because
they are the same, and (2) when we observe table 1 we notice that the words
in the code that constitute an optimal solution to the problems are complementary
in pairs. This is a property of optimal solutions to the ECC problem
as we will demonstrate in the following lines.
Let consider as an hypothesis that x0
is an optimal solution to the ECC problem where x0 is made
of M words (P1,...,PM) with M-2
words of that code obeying the property described above and the two
remaining words
(Pa and Pb) are not complementary in x
bits position (x>0). The equation for the fitness function would
be:
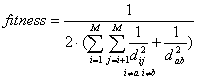 (Eq. 2)
(Eq. 2)
where
![]() (Eq. 3)
(Eq. 3)
If we replace the word Pb in S0 with Pc such that Pa and Pc are complementary too, the fitness function for the new formed up solution S1 would be:
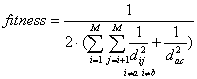 (Eq. 4)
(Eq. 4)
where
![]() (Eq. 5)
(Eq. 5)
At the beginning of this demonstration, we supposed that S0 was an optimal solution to the problem, so we have that:
![]() (Eq. 6)
(Eq. 6)
and therefore:
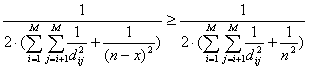 (Eq. 7)
(Eq. 7)
![]() (Eq.
8)
(Eq.
8)
In equation 8, x was supposed to be an integer and
n is the number of bits in every word of the code and it is an
integer too, so equation 8 is a contradiction and our hypothesis is confirm
not to be true. We can conclude that for an
optimal solution to the ECC problem it is necessary that words constituting
the code are complementary in pairs.
If we consider the property shown before, the problem parameters
are changed because in this case we only have to find M/2 and afterwards
we easily generate the remaining M/2 complementary words to have a complete
code by a simple transformation which is applied in equation 9.
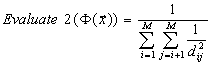 ( Eq. 9)
( Eq. 9)
We have to notice then, that function Evaluate2 which incorporates
the two improvements shown before, has a different input from Evaluate1. The
differences between Evaluate1 and Evaluate2 can be observed in table 2 where
psedo-codes for both function are shown in a C-like style.
See in table 3 the numeric ranges returned by each
of the maximized functions.
| double evaluate1 (int x[N], int N); { int d; double sum, fitness; for (i=1; i<=M; i++) for (j=1; j<=M; j++) if (i!=j) { d=compute_hamming_distance(x,i,j); sum=sum+1/power(d,2); } fitness=1/sum; return fitness; } |
| double evaluate2 (int x[N/2], int N/2); { int d, c, newx[N]; double sum, fitness; for (c=1; c<=N/2; c++) { newx[c]=x[c]; newx[N/2+c]=1-x[c]; } for (i=1; i<=M; i++) for (j=i+1; j<=M; j++) { d=compute_hamming_distance(x,i,j); sum=sum+1/power(d,2); } fitness=1/(sum*2); return fitness; } |
Table 2. Pseudo-code for the two evaluation function being compared.
| Functions | Ranges |
| Evaluate1 | [0,0.0674] |
| Evaluate1 | [0,0.0674] |
Table 3. Numeric ranges returned by Evaluate1 and Evaluate2.
| Home | Introduction on EAs | xxGA | Problems | Links | Articles DB |