RLFAP Problem Description
The Radio Link Frequency Assignment Problem is that of assigning frequencies to a number of radio links in such a manner as to simultaneously satisfy a large number of constraints and use as few distinct frequencies as possible. This problem is known to be NP-complete.
This study is based on the article Using Genetic Algorithms to solve the Radio Link Frequency Assignment Problem presented by A. Kapsalis, V. J. Rayward-Smith and G. D. Smith from the School of Information Systems at the University of East Anglia in Norwich in the international conference Artificial Neural Nets and Genetic Algorithms in Alès, France in 1995.
The RLFAP problem can be stated as follows: We are given a set of links that have to be assigned frequencies. Typically, there may be of the order of 200 to 1000 links and approximately 50 discrete frequency values, so the latter are assigned to many different links. As a result, interference considerations generate many constraints. We have to find a feasible solution, i.e. one that satisfies all given constraints and on top of that he have to find and optimal solution by minimizing some cost function.
Formally, each link 
is
assigned a frequency value fi from a given domain Di,
which is a subset of all available frequency values. For the particular problem
type we are studying, there exist a large number of interference constraints
of the following types: for a given pair of links i and j, it
is necessary that:
(Eq. 1)
(Eq. 2)
Let N be the number of variables in the problem. An assignment is represented by a string of frequencies fi,
|
f1 |
f2 |
f3 |
... |
... |
fn |
where fi is a frequency in domain Di, i.e. the domain associated with link / variable i.
For each given assignment it is possible to determine:
The number of distinct frequency values assigned, D.
The number of equality constraints violated, EC.
The number of inequality constraints violated, IC.
From this result the cost function
(Eq. 3)
(Eq. 4)
The value of the penalty parameter is determined by any of the following mechanisms:
Number of links 'not assigned' - Whenever, a constraint is violated, the two variables with are marked as 'not assigned'. The weighted total of the number of links 'not assigned is added to the fitness function.
Constraint weighting by degree - For each constraint, a positive weight is determined, based on the number of times each of the links appears in the list of constraints. When evaluating a solution, a term equal to the sum of the weights for the violated constraints is added to the fitness as a penalty.
Constraint by frequency pair - This worked in the same way as the previous method, but in this case, the weights were determined by the number of frequency pairs that satisfy each of the constraints.
Dynamic constraints violation weights - Every time a new solution is evaluated, a set of counters, one for each constraint, is updated according to which constraints were violated. After r generations, the counters are used to determine weights for all constraints, the constraints that is violated most being assigned the highest weight. The fitness function is augmented by a term in the same manner as in the static constraint weighting.
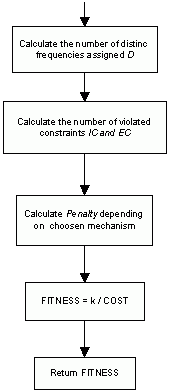
Figure 1. Evaluate function flow diagram
 |
Home | Introduction on EAs | xxGA | Problems | Links | Articles DB |  |