TA Problem Description
The objective of the terminal assignment (TA) problem involves determining minimum cost links to form a network by connecting a given collection of terminals to a given collection of concentrators. The terminal sites and concentrators sites have fixed locations and are known. The capacity requirement of each terminal is known and may vary from one terminal to another. The capacities of all concentrators and the cost of linking each terminal to a concentrator are also known. The problem is now to identify for each terminal the concentrator to which it should be assigned, under two constraints, in order to minimize the total cost. The two constraints imposed on the TA problem are:(1) each terminal must be connected to one and only one to the concentrators, and (2) the aggregate capacity requirement of the terminals connected to any one concentrator must not exceed the capacity of that concentrator. The intractability of this problem is a motivation for the pursuits of heuristics that produce approximate, rather than exact, solutions.
We will work with the following terms:
|
Terminals |
(l1,l2,...,l T) |
| Weights | (w1,w2,...,w T) |
| Concentrators | (r1,r2,...,r C) |
| Capacities | (p1,p2,...,p C) |
wi is the weight, or capacity requirements of terminal li. The weights and capacity are positive integers and wi is smaller or equal to min {p1, p 2, ..., pC} for i=1,2,...,T. The T terminals and the C concentrators are place on the Euclidean grid, i.e., li has coordinates (li1,li2) and ri has coordinates (rj1,rj2).
A feasible solution is
to assign each terminal to one of the concentrators such that no concentrator
exceeds its capacity. In other words, a feasible solution to the terminal assignment
problem is a vector ![]() where xi=j means that the ith terminal is assigned to the
concentrator j such that
where xi=j means that the ith terminal is assigned to the
concentrator j such that ![]() and xi is an integer, for i=1,2,...,T, (i.e.,
all terminals have to be assigned) and
and xi is an integer, for i=1,2,...,T, (i.e.,
all terminals have to be assigned) and ![]() for j=1,2,...,C (i.e., capacity of concentrator is not exceeded)
where
for j=1,2,...,C (i.e., capacity of concentrator is not exceeded)
where ![]() i.e., Rj represents the terminals that are assigned to concentrator
j.
i.e., Rj represents the terminals that are assigned to concentrator
j.
The objective function is:
![]() (Eq.1)
(Eq.1)
where
![]()
![]() (Eq. 2)
(Eq. 2)
i.e., the result of rounding the distance between terminal i and concentrator j. In other words, Z denotes the overall cost of assigning individual terminals to concentrators according to the solution represented by vector x.
The data problem instances for this study were taken the article Heuristic Algorithms for the Terminal Assignment Problem, published by Sami Khuri and Teresa Chiu from the Computer Science and Mathematical Department at the University of the state of San Jose (U.S.A.).
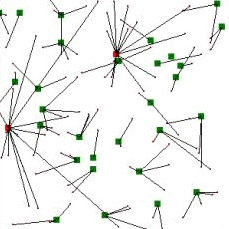 |
|
Overload =2
|
Figure1. Graphical representation of a non feasible solution
to the problem.
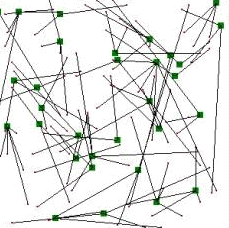 |
|
Overload = 0 |
Figure2. Graphical representation of a feasible solution to the problem.
Pictures above represents two different solutions to the terminal assignment problem, the first one is not actually a solution, because it is a not feasible solution, that means we have some overloaded concentrators which are in red. Non overloaded concentrators are in green and terminals are represented by small black dots. A connection between a terminal and a concentrator is represented by a edge.
And here behind, we can find a flow diagram for the Evaluate function we have used to try to solve this problem.
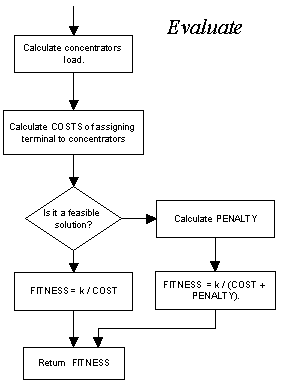
Figure 3. Evaluate function flow diagram.
| Home | Introduction on EAs | xxGA | Problems | Links | Articles DB |