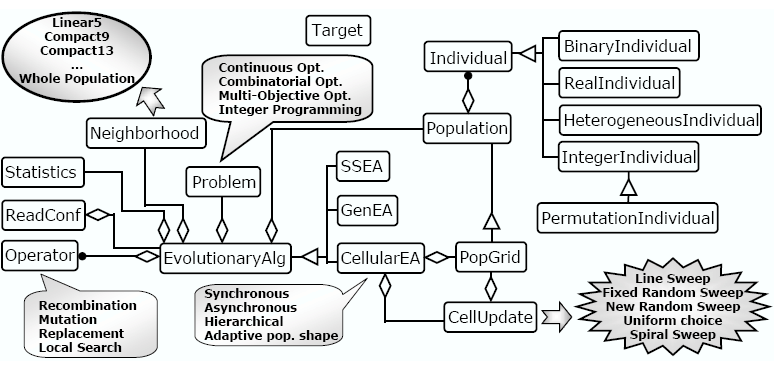
In the figure below we show a summarized UML diagram describing the design of JCell. As can be seen, the main class of the design is the so called EvolutionaryAlg, which is a generic class for the design of evolutionary algorithms, and holds all the parameter configuration of the algorithm. This class has an abstract method in charge of executing the breeding loop of the EA. Thus, we defined the classes SSEA, GenEA, and CellularEA for implementing a steady-state, a generational, and a cellular EA, respectively, just by extending that method.
ReadConf is the class in charge of reading all the required parameterization from the configuration file, and set the corresponding values to the parameters of EvolutionaryAlg. Thus, the first thing we have to do when using this framework in our program must be a call to ReadConf with the path to a configuration file wherein the desired parameterization of the algorithm is given. The structure of this configuration file is described here.
The class EvolutionaryAlg contains instantiations of classes Population, Neighborhood, Problem, Operator, and Statistics. Additionally, EvolutionaryAlg also holds several important parameters (which values are set by ReadConf), some of them common to all the implemented EAs, such as the probabilities of applying recombination, mutation, and local search operators, and the termination condition, and some of them specific to any kind of EA, like the synchronicity of individuals update in the population (synchronous or asynchronous update policies) for the cellular EA.
Population contains a lineal list of Individual objects. Individual is the class of JCell implementing a generic individual of an EA. Depending on the genotype information hold by the individual, it can be instantiated as a BinaryIndividual, RealIndividual, IntegerIndividual, HeterogeneousIndividual, or PermutationIndividual. This last one is an IntegerIndividual in which the values of the genes are a permutation of integer numbers. A summary of the different kinds of individual available in JCell is given in Table 1. The fitness value of an individual is an array of Double objects. This array has length 1 when we are solving problems with only one function to optimize, and n in the case of multi-objective optimization (n being the number of objectives).

Table 1. Individuals implemented in JCell.
As it was already explained, one distinguishing feature of cellular EAs is that the population is structured by establishing some neighboring relations to the individuals in the population. Thus, Neighborhood is a generic class for obtaining the neighbors of a given individual, and therefore any specific neighborhood to be implemented in JCell must inherit from this class. Specifically, the Linear5, Compact9, and Compact13 neighborhoods are implemented in JCell. In the case of the steady-state and the generational EAs, the neighborhood is composed by the whole population.
Every problem we want to solve using JCell must be implemented in a class inheriting from the class Problem. This class is generic enough for allowing the use of problems belonging to such different fields like combinatorial, continuous, integer programming, or even multi-objective optimization. The use of constraints is possible in any of the previous problem domains. Additionally, the variable values can be restricted to a given interval for each gene. A subclass of Problem must contain every information needed about the considered problem, such as the number of variables, which can be different to the length of the chromosome since it is possible to code one variable with more than one gene, the number of constraints, the best known fitness value to the problem (only for single-objective optimization), and the interval of allowed values for each gene.
An EvolutionaryAlg object has a pool of Operator objects. This generic class is used for implementing all the EA operators, i.e., the selection method for each of the parents, the recombination and mutation operators, the (optional) local search step, and the replacement policy for the newly generated individuals.
At every generation, the algorithm call the Statistics class. Computing basic statistics is rarely found in the codes of other authors. However, it is an essential step for the work and monitoring of the algorithm. In fact, it is possible to use some kind of statistical descriptors in some of the new algorithmic improvements we propose in this dissertation, e.g. to guide an adaptive search.
As it was said before, CellularEA is the class for implementing
cEAs in our framework. This class contains a PopGrid and a
CellUpdate object. PopGrid is an extended
class of Population, and it is needed for giving a 2-dimensional
structure to the population. The other class, CellUpdate, is
used for defining the visiting order of the individuals during the breeding
loop. Specifically, the Line Sweep, Fixed Random Sweep,
New Random Sweep, Uniform Choice, and Spiral
Sweep policies are supported. Additionally, the CellularEA
class
allows the user to specify whether a hierarchy should be applied to the population,
and/or the population shape should change during the run for auto-adapting the
selection pressure.
There is also a static class called Target which holds a boolean variable, called maximize, for storing whether the algorithm is maximizing or minimizing. Additionally, this class is used for making all the comparisons between both individuals and fitness values, deciding the best one in terms of the value of variable maximize. Thus, all the comparisons between individuals and fitness values are a black box for the rest of classes of JCell, so these classes call the same method independently of maximizing or minimizing, if we are holding constraints or not, or even if we are solving a single-objective or multi-objective problem. In this last case, the terms better or worse are not directly applied, the concepts of dominating (considered as better), dominated (worse), and non-dominated (non-worse) individuals are used instead in the comparisons inside Target.
Finally, we would like to remark that it is very easy to extend this framework by, for example, adding the chance of having more than one chromosome into individuals, using other different data types for the genes, or even implementing other kinds of EAs, such as GP, ES, EDA, or PSO.